��Ŀ����
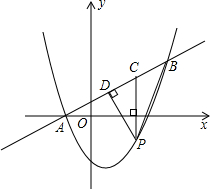 ��2012•���ϣ���ͼ����ƽ��ֱ������ϵ�У�ֱ��y=
��2012•���ϣ���ͼ����ƽ��ֱ������ϵ�У�ֱ��y=| 1 | 2 |
��1����a��b��sin��ACP��ֵ��
��2�����P�ĺ�����Ϊm��
���ú���m�Ĵ���ʽ��ʾ�߶�PD�ij���������߶�PD�������ֵ��
������PB���߶�PC�ѡ�PDB�ֳ����������Σ��Ƿ�����ʺϵ�m��ֵ��ֱ��д��m��ֵ��ʹ�����������ε����֮��Ϊ9��10�������ڣ�ֱ��д��m��ֵ���������ڣ�˵�����ɣ�
��������1����ֱ֪��AB�Ľ���ʽ��������ȷ��A��B������꣬Ȼ�����ô���ϵ����ȷ��a��b��ֵ������ֱ��AB��y��Ľ���ΪE��E��������֪����Rt��AEO�У������sin��AEO������AEO=��ACP�����ACP������ֵ�ɵã�
��2������֪P������꣬����ֱ��AB�������ߵĽ���ʽ�����C��P�����꣬�ɴ˵õ��߶�PC�ij�����Rt��PCD�У����ݣ�1���С�ACP������ֵ���������PD�ı���ʽ���ٸ������ú������������PD�������ֵ��
���ڱ����PCD����PBC�����ʱ��������PCΪ�ף���ô���ǵ�����ȵ���PC���ϵĸߵıȣ��ֱ��B��D��PC�Ĵ��ߣ�����������������߶εı���ʽ��Ȼ�������ɸ��������������ϵ���m��ֵ��
��2������֪P������꣬����ֱ��AB�������ߵĽ���ʽ�����C��P�����꣬�ɴ˵õ��߶�PC�ij�����Rt��PCD�У����ݣ�1���С�ACP������ֵ���������PD�ı���ʽ���ٸ������ú������������PD�������ֵ��
���ڱ����PCD����PBC�����ʱ��������PCΪ�ף���ô���ǵ�����ȵ���PC���ϵĸߵıȣ��ֱ��B��D��PC�Ĵ��ߣ�����������������߶εı���ʽ��Ȼ�������ɸ��������������ϵ���m��ֵ��
��� �⣺��1����
�⣺��1����
x+1=0����x=-2����A��-2��0����
��
x+1=3����x=4����B��4��3����
��y=ax2+bx-3����A��B���㣬
��
��
��
�������ߵĽ���ʽΪ��y=
x2-
x-3��
��ֱ��AB��y�ύ�ڵ�E����E��0��1����
��PC��y�ᣬ
���ACP=��AEO��
��sin��ACP=sin��AEO=
=
=
��
��2�����ɣ�1��֪�������ߵĽ���ʽΪy=
x2-
x-3�����P��m��
m2-
m-3����
��ֱ֪��AB��y=
x+1�����C��m��
m+1����
��PC=
m+1-��
m2-
m-3��=-
m2+m+4=-
��m-1��2+
Rt��PCD�У�PD=PC•sin��ACP=[-
��m-1��2+
]•
=-
��m-1��2+
��PD�������ֵΪ��
��
 ����ͼ���ֱ����D��B��DF��PC��BG��PC������ֱ�ΪF��G��
����ͼ���ֱ����D��B��DF��PC��BG��PC������ֱ�ΪF��G��
��sin��ACP=
��
��cos��ACP=
��
�֡ߡ�FDP=��ACP
��cos��FDP=
=
��
��Rt��PDF��DF=
PD=-
��m2-2m-8����
�֡�BG=4-m��
��
=
=
=
��
��
=
=
ʱ�����m=
��
��
=
=
ʱ�����m=
��
 �⣺��1����
�⣺��1����| 1 |
| 2 |
��
| 1 |
| 2 |
��y=ax2+bx-3����A��B���㣬
��
|
��
|
�������ߵĽ���ʽΪ��y=
| 1 |
| 2 |
| 1 |
| 2 |
��ֱ��AB��y�ύ�ڵ�E����E��0��1����
��PC��y�ᣬ
���ACP=��AEO��
��sin��ACP=sin��AEO=
| OA |
| AE |
| 2 | ||
|
2
| ||
| 5 |
��2�����ɣ�1��֪�������ߵĽ���ʽΪy=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
��ֱ֪��AB��y=
| 1 |
| 2 |
| 1 |
| 2 |
��PC=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 9 |
| 2 |
Rt��PCD�У�PD=PC•sin��ACP=[-
| 1 |
| 2 |
| 9 |
| 2 |
2
| ||
| 5 |
| ||
| 5 |
9
| ||
| 5 |
��PD�������ֵΪ��
9
| ||
| 5 |
 ����ͼ���ֱ����D��B��DF��PC��BG��PC������ֱ�ΪF��G��
����ͼ���ֱ����D��B��DF��PC��BG��PC������ֱ�ΪF��G����sin��ACP=
2
| ||
| 5 |
��cos��ACP=
| 1 | ||
|
�֡ߡ�FDP=��ACP
��cos��FDP=
| DF |
| DP |
| 1 | ||
|
��Rt��PDF��DF=
| 1 | ||
|
| 1 |
| 5 |
�֡�BG=4-m��
��
| S��PCD |
| S��PBC |
| DF |
| BG |
-
| ||
| 4-m |
| m+2 |
| 5 |
��
| S��PCD |
| S��PBC |
| m+2 |
| 5 |
| 9 |
| 10 |
| 5 |
| 2 |
��
| S��PCD |
| S��PBC |
| m+2 |
| 5 |
| 10 |
| 9 |
| 32 |
| 9 |
���������⿼���˶��κ�����Ӧ���Լ�����ʽ��ȷ������ֱ�������Ρ�ͼ���������֪ʶ����Ҫ����ѧ�����ν��˼���Ӧ��������

��ϰ��ϵ�д�
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
�����Ŀ
 ��2012•���ϣ���ͼ��ʾ�ļ����������ͼ�ǣ�������
��2012•���ϣ���ͼ��ʾ�ļ����������ͼ�ǣ������� ME������CD�ڵ�N������MD��AN��
ME������CD�ڵ�N������MD��AN�� ��2012•���ϣ���ͼ����֪AB�ǡ�O��ֱ����AD�С�O�ڵ�A��
��2012•���ϣ���ͼ����֪AB�ǡ�O��ֱ����AD�С�O�ڵ�A��
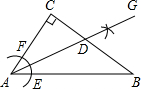 ��2012•���ϣ���ͼ���ڡ�ABC�У���C=90�㣬��CAB=50�㣮�����²�����ͼ�����Ե�AΪԲ�ģ�С��AC�ij�Ϊ�뾶�������ֱ�AB��AC�ڵ�E��F���ڷֱ��Ե�E��FΪԲ�ģ�����
��2012•���ϣ���ͼ���ڡ�ABC�У���C=90�㣬��CAB=50�㣮�����²�����ͼ�����Ե�AΪԲ�ģ�С��AC�ij�Ϊ�뾶�������ֱ�AB��AC�ڵ�E��F���ڷֱ��Ե�E��FΪԲ�ģ�����