题目内容
已知：如图，矩形DEFG内接于△ABC，AH⊥BC于H，若AH=4cm，BC=12cm，ED：EF=1：2，则EF=分析：先根据ED：EF=1：2设出ED=a，则EF=2a，再根据△AEF∽△ABC，利用相似三角形的性质解答．
解答：解：本题中已知ED：EF=1：2，可以设ED=a，则EF=2a，
根据条件AM=4-a，
由已知条件得到△AEF∽△ABC，
则
=
，
得到
=
，
解得a=2.4，
则EF=4.8cm．
根据条件AM=4-a，
由已知条件得到△AEF∽△ABC，
则
| EF |
| BC |
| AM |
| AH |
得到
| 2a |
| 12 |
| 4-a |
| 4 |
解得a=2.4，
则EF=4.8cm．
点评：本题考查对相似三角形性质的理解，相似三角形对应高的比等于相似比．
练习册系列答案
相关题目
22、已知：如图，矩形ABCD的对角线AC与BD相交于点O，点O关于直线AD的对称点是E，连接AE、DE．
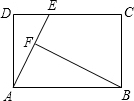
26、已知：如图，矩形ABCD中，BC延长线上一点E满足BE=BD，F是DE的中点，猜想∠AFC的度数并证明你的结论．
（2002•西藏）已知：如图，矩形ABCD中，E、F是AB边上两点，且AF=BE，连结DE、CF得到梯形EFCD．