Question

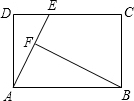
已知：如图，矩形ABCD中，AB=5，AD=3，E是CD上一点（不与C、D重合），连接AE，过点B作BF⊥AE，垂足为F．
（1）若DE=2，求cos∠ABF的值；
（2）设AE=x，BF=y，①求y关于x之间的函数关系式，写出自变量x的取值范围；②问当点E从D运动到C，BF的值在增大还是减小？并说明理由．
（3）当△AEB为等腰三角形时，求BF的长．

Answer 1

分析：（1）直接根据相似三角形的判定得出△ABF∽△EDA，再利用成比例线段可知

BF

AB

=

AD

AE

=

3 13

13

，即可得出答案；
（2）①直接利用（1）中结果表示为：y=

15

x

；②其利用其单调性可知：y随x的增大而减小．
（3）当△AEB为等腰三角形时，有3种情况：a、当AB=BE时，BF=

3 10

2

b、当AE=BE时，BF=

30 61

61

c、当AB=AE=5时，BF=AD=3．

解答：解：（1）∵BF⊥AE，
∴∠FBA+∠FAB=90°，∠AFB=90°，
∵∠D=∠AFB=90°，
∵∠DAE+∠EAB=90°，
∴∠FBA=∠EAD，
∴△ABF∽△EDA
∵DE=2，AD=3，
∴AE=

13

，
∴cos∠ABF=

BF

AB

=

AD

AE

=

3 13

13

；

（2）根据（1）可知：
①

5

x

=

y

3

即y=

15

x

，3＜x＜

34

；
②减小，因为y=

15

x

中，每个象限内，y随x的增大而减小；

（3）当△AEB为等腰三角形时，有3种情况：
a、当AB=BE时，则BE=5，则CE=

BE2-BC2

=4，∴DE═5-4=1，
∴AE=

AD2+DE2

=

10

，
∴AF=

10

2

，
∴BF=

3 10

2

；
b、当AE=BE时，E为CD中点，则DE=2.5，AE=

61

2

，
∵AD•AB=BF•AE，
∴3×5=BF×

61

2

，
∴BF=

30 61

61

；
c、当AB=AE=5时，△ABF≌△AED，则BF=AD=3．
所以BF的值为：

3 10

2

或

30 61

61

或3．

点评：此题主要考查了反比例函数和矩形的综合题．解题的关键是熟练掌握矩形的性质和反比例函数的关系式的几何意义．在解决第三问时要把三种情况都考虑进去，不要漏掉一种情况，灵活运用三角形相似或勾股定理解题．