Question

22、已知：如图，矩形ABCD的对角线AC与BD相交于点O，点O关于直线AD的对称点是E，连接AE、DE．
（1）试判断四边形AODE的形状，不必说明理由；
（2）请你连接EB、EC，并证明EB=EC．

Answer 1

分析：（1）利用对称的性质，又因为四边形ABCD是矩形，两个结论联合起来，可知四边形AODE是菱形，（2）先证出∠EAB=∠EDC，再证明△EAB≌△EDC，从而得出EB=EC．

解答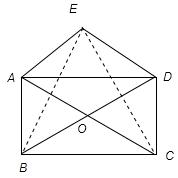：解：（1）∵点O和点E关于直线AD对称，
∴AOD≌△AED；
∴OA=OE  OD=DE；
∵有矩形ABCD，
∴OA=OD；
∴OA=OD=DE=EA；
∴四边形AODE是菱形．

（2）∵四边形AODE是菱形，
∴AE=ED；
∴∠EAD=∠EDA；
∵四边形ABCD是矩形，
∴AB=CD，∠BAD=∠CDA=90°；
∴∠EAD+∠BAD=∠EDA+∠CDA；
∴∠EAB=∠EDC；
∴△EAB≌△EDC；
∴EB=EC．

点评：本题利用对称的性质（对称图形全等）和矩形的性质（矩形的对角线互相平分），以及全等三角形的判定和性质．