题目内容
已知二次函数y=ax2+bx(a≠0),当x取x1,x2(x1≠x2)时,函数值相等,求当x取x1+x2时的函数值.
考点:二次函数的性质,二次函数图象上点的坐标特征
专题:计算题
分析:由于ax12+bx1=ax22+bx2,移项后分解得到(x1-x2)(ax1+ax2+b)=0,而x1≠x2,所以ax1+ax2+b=0,即x1+x2=-
,然后把x=-
代入二次函数解析式中计算即可.
| b |
| a |
| b |
| a |
解答:解:根据题意得ax12+bx1=ax22+bx2,
ax12-ax22+bx1-bx2=0,
a(x1-x2)(x1+x2)+b(x1-x2)=0,
(x1-x2)(ax1+ax2+b)=0,
∵x1≠x2,
∴ax1+ax2+b=0,即x1+x2=-
,
∴当x=x1+x2=-
时,y=a×(-
)2+b×(-
)=0.
ax12-ax22+bx1-bx2=0,
a(x1-x2)(x1+x2)+b(x1-x2)=0,
(x1-x2)(ax1+ax2+b)=0,
∵x1≠x2,
∴ax1+ax2+b=0,即x1+x2=-
| b |
| a |
∴当x=x1+x2=-
| b |
| a |
| b |
| a |
| b |
| a |
点评:本题考查了二次函数的性质:二次函数y=ax2+bx+c(a≠0)的顶点坐标是(-
,
),对称轴直线x=-
,二次函数y=ax2+bx+c(a≠0)的图象具有如下性质:①当a>0时,抛物线y=ax2+bx+c(a≠0)的开口向上,当x<-
时,y随x的增大而减小;x>-
时,y随x的增大而增大;x=-
时,y取得最小值
,即顶点是抛物线的最低点.②当a<0时,抛物线y=ax2+bx+c(a≠0)的开口向下,x<-
,y随x的增大而增大;x>-
时,y随x的增大而减小;当x=-
时,y取得最大值
,即顶点是抛物线的最高点.
| b |
| 2a |
| 4ac-b2 |
| 4a |
| b |
| 2a |
| b |
| 2a |
| b |
| 2a |
| b |
| 2a |
| 4ac-b2 |
| 4a |
| b |
| 2a |
| b |
| 2a |
| b |
| 2a |
| 4ac-b2 |
| 4a |

练习册系列答案
相关题目
设x=
,则x的值满足( )
| 13 |
| A、1<x<2 |
| B、2<x<3 |
| C、3<x<4 |
| D、4<x<5 |
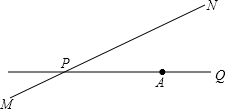 如图,公路MN和公路PQ在点P处交汇且∠QPN=30°,点A处有一所中学,AP=160m.假设拖拉机行驶时,周围100m以内会受到噪音的影响(已知拖拉机的速度为18km/h),那么拖拉机在公路MN上眼PN方向行驶时,学校收到噪声影响的时间为多少秒?
如图,公路MN和公路PQ在点P处交汇且∠QPN=30°,点A处有一所中学,AP=160m.假设拖拉机行驶时,周围100m以内会受到噪音的影响(已知拖拉机的速度为18km/h),那么拖拉机在公路MN上眼PN方向行驶时,学校收到噪声影响的时间为多少秒? 正方形ABCD中,G为CD上一点,以CG为边作正方形GFEC,求证:BG⊥DE.
正方形ABCD中,G为CD上一点,以CG为边作正方形GFEC,求证:BG⊥DE.