题目内容
已知:y关于x的函数
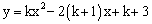 的图象与x轴有交点。
的图象与x轴有交点。
(1)求k的取值范围;
(2)若x1,x2是函数图象与x轴两个交点的横坐标,且满足 .
.
①求k的值;②当 时,请结合函数图象确定y的最大值和最小值。
时,请结合函数图象确定y的最大值和最小值。
(1)当k=0时,函数为一次函数y=﹣2x+3,其图象与x轴有一个交点。
当k≠0时, 函数为二次函数,其图象与x轴
函数为二次函数,其图象与x轴 有一个或两个交点,
有一个或两个交点,
令y=0得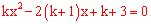 .
.
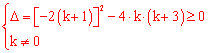 ,解得
,解得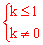 。
。
综上所述,k的取值范围是k≤1。
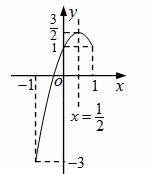 (2)①∵x1≠x2,由(1)知k<1且k≠0。
(2)①∵x1≠x2,由(1)知k<1且k≠0。
由题意得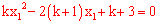 ,即
,即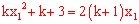 (*),
(*),
将(*)代入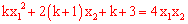 中得:
中得: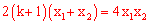 。
。
又∵x1+x2=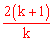 ,x1x2=
,x1x2=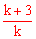 ,∴
,∴ ,
,
解得:k1=﹣2,k2=1(不合题意,舍去)。∴所求k值为﹣2。
②如图,∵k=﹣2,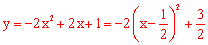 ,且﹣1≤x≤1,
,且﹣1≤x≤1,
由图象知:当x=﹣1时,y最小=﹣ 3;当x=
3;当x=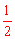 时,y最大=
时,y最大=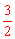 。
。
∴y的最大值为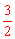 ,最小值为﹣3。
,最小值为﹣3。
【考点】抛物线与x轴的交点,一次函数的定义,一元二次方程根的判别式和根与系数物关系,二次函数的最值,分类思想和数形结合思想的应用。


练习册系列答案
相关题目
 、
、 b为非负实数,则当代数式
b为非负实数,则当代数式
 取得最小值时,
取得最小值时, = 。
= 。 D。
D。
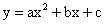
 过点B。
过点B。 、M、N,线段MN的垂直平分线l过点C,交线段OA于点F。当AF=1时,求抛物线的解析式。
、M、N,线段MN的垂直平分线l过点C,交线段OA于点F。当AF=1时,求抛物线的解析式。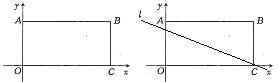
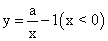 的图象如图,那么关于x的分式方程
的图象如图,那么关于x的分式方程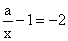 的解是【 】
的解是【 】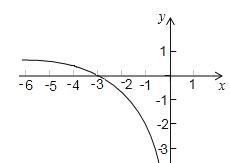
 1 B.x=
1 B.x= 针落在哪
针落在哪 一区域就可以获得相应的奖品.下表是活动进
一区域就可以获得相应的奖品.下表是活动进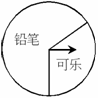



 BP=
BP= 

 B重合),OD⊥BC,OE⊥AC,垂足分别为D,E,则DE的长度( )
B重合),OD⊥BC,OE⊥AC,垂足分别为D,E,则DE的长度( )

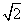
 D.
D.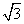

 旋转45
旋转45 方形ODEF设为正方形PQMN,如图3,设正方形PQMN移动的时间为x秒,正方形PQMN与正方形OABC的重叠部分面积为y,直接写出y与x之间的函数解析式;
方形ODEF设为正方形PQMN,如图3,设正方形PQMN移动的时间为x秒,正方形PQMN与正方形OABC的重叠部分面积为y,直接写出y与x之间的函数解析式;