题目内容
平面直角坐标系xOy中,点A、B分别在函数y1=
(x>0)与y2=-
(x<0)的图象上,A、B的横坐标分别为
a、b.

(1)若AB∥x轴,求△OAB的面积;
(2)若△OAB是以AB为底边的等腰三角形,且a+b≠0,求ab的值;
(3)作边长为3的正方形ACDE,使AC∥x轴,点D在点A的左上方,那么,对大于或等于4的任意实数a,CD边与函数y1=
(x>0)的图象都有交点,请说明理由.
| 4 |
| x |
| 4 |
| x |
a、b.

(1)若AB∥x轴,求△OAB的面积;
(2)若△OAB是以AB为底边的等腰三角形,且a+b≠0,求ab的值;
(3)作边长为3的正方形ACDE,使AC∥x轴,点D在点A的左上方,那么,对大于或等于4的任意实数a,CD边与函数y1=
| 4 |
| x |
考点:反比例函数综合题
专题:代数几何综合题,压轴题
分析:(1)如图1,AB交y轴于C,由于AB∥x轴,根据k的几何意义得到S△OAC=2,S△OBC=2,所以S△OAB=S△OAC+S△OBC=4;
(2)根据函数图象上点的坐标特征得A、B的纵坐标分别为
、-
,根据两点间的距离公式得到OA2=a2+(
)2,OB2=b2+(-
)2,则利用等腰三角形的性质得到a2+(
)2=b2+(-
)2,变形得到(a+b)(a-b)(1-
)=0,由于a+b≠0,a>0,b<0,所以1-
=0,易得ab=-4;
(3)由于a≥4,AC=3,则可判断直线CD在y轴的右侧,直线CD与函数y1=
(x>0)的图象一定有交点,设直线CD与函数y1=
(x>0)的图象交点为F,由于A点坐标为(a,
),正方形ACDE的边长为3,则得到C点坐标为(a-3,
),F点的坐标为(a-3,
),所以FC=
-
,然后比较FC与3的大小,由于3-FC=3-(
-
)=
,而a≥4,所以3-FC≥0,于是可判断点F在线段DC上.
(2)根据函数图象上点的坐标特征得A、B的纵坐标分别为
| 4 |
| a |
| 4 |
| b |
| 4 |
| a |
| 4 |
| b |
| 4 |
| a |
| 4 |
| b |
| 16 |
| a2b2 |
| 16 |
| a2b2 |
(3)由于a≥4,AC=3,则可判断直线CD在y轴的右侧,直线CD与函数y1=
| 4 |
| x |
| 4 |
| x |
| 4 |
| a |
| 4 |
| a |
| 4 |
| a-3 |
| 4 |
| a-3 |
| 4 |
| a |
| 4 |
| a-3 |
| 4 |
| a |
| 3(a+1)(a-4) |
| a(a-3) |
解答: 解:(1)如图1,AB交y轴于C,
解:(1)如图1,AB交y轴于C,
∵AB∥x轴,
∴S△OAC=
×|4|=2,S△OBC=
×|-4|=2,
∴S△OAB=S△OAC+S△OBC=4;
(2)∵A、B的横坐标分别为a、b,
∴A、B的纵坐标分别为
、-
,
∴OA2=a2+(
)2,OB2=b2+(-
)2,
∵△OAB是以AB为底边的等腰三角形,
∴OA=OB,
∴a2+(
)2=b2+(-
)2,
∴a2-b2+(
)2-(
)2=0,
∴a2-b2+
=0,
∴(a+b)(a-b)(1-
)=0,
∵a+b≠0,a>0,b<0,
∴1-
=0,
∴ab=-4;
(3)∵a≥4,
而AC=3,
∴直线CD在y轴的右侧,直线CD与函数y1=
(x>0)的图象一定有交点,
设直线CD与函数y1=
(x>0)的图象交点为F,如图2,
∵A点坐标为(a,
),正方形ACDE的边长为3,
∴C点坐标为(a-3,
),
∴F点的坐标为(a-3,
),
∴FC=
-
,
∵3-FC=3-(
-
)=
,
而a≥4,
∴3-FC≥0,即FC≤3,
∵CD=3,
∴点F在线段DC上,
即对大于或等于4的任意实数a,CD边与函数y1=
(x>0)的图象都有交点.
 解:(1)如图1,AB交y轴于C,
解:(1)如图1,AB交y轴于C,∵AB∥x轴,
∴S△OAC=
| 1 |
| 2 |
| 1 |
| 2 |
∴S△OAB=S△OAC+S△OBC=4;
(2)∵A、B的横坐标分别为a、b,
∴A、B的纵坐标分别为
| 4 |
| a |
| 4 |
| b |
∴OA2=a2+(
| 4 |
| a |
| 4 |
| b |
∵△OAB是以AB为底边的等腰三角形,
∴OA=OB,
∴a2+(
| 4 |
| a |
| 4 |
| b |
∴a2-b2+(
| 4 |
| a |
| 4 |
| b |
∴a2-b2+
| 16(b2-a2) |
| a2b2 |
∴(a+b)(a-b)(1-
| 16 |
| a2b2 |
∵a+b≠0,a>0,b<0,
∴1-
| 16 |
| a2b2 |
∴ab=-4;
(3)∵a≥4,
而AC=3,
∴直线CD在y轴的右侧,直线CD与函数y1=
| 4 |
| x |

设直线CD与函数y1=
| 4 |
| x |
∵A点坐标为(a,
| 4 |
| a |
∴C点坐标为(a-3,
| 4 |
| a |
∴F点的坐标为(a-3,
| 4 |
| a-3 |
∴FC=
| 4 |
| a-3 |
| 4 |
| a |
∵3-FC=3-(
| 4 |
| a-3 |
| 4 |
| a |
| 3(a+1)(a-4) |
| a(a-3) |
而a≥4,
∴3-FC≥0,即FC≤3,
∵CD=3,
∴点F在线段DC上,
即对大于或等于4的任意实数a,CD边与函数y1=
| 4 |
| x |
点评:本题考查了反比例函数的综合题:掌握反比例函数图象上点的坐标特征、反比例函数比例系数的几何意义、图形与坐标和正方形的性质;会利用求差法对代数式比较大小.

练习册系列答案
相关题目
下列四个实数中,是无理数的为( )
| A、0 | ||
| B、-3 | ||
C、
| ||
D、
|
抛物线y=2(x-3)2+4的对称轴是( )
| A、直线x=-3 |
| B、直线x=4 |
| C、直线x=3 |
| D、直线x=2 |
 如图,在Rt△ABC中,∠ACB=90°,以AC为直径作⊙O交AB于点D点,连接CD.
如图,在Rt△ABC中,∠ACB=90°,以AC为直径作⊙O交AB于点D点,连接CD.
 已知Rt△ABO中,AB=OB=2,∠ABO=90°.以AB为边,在Rt△ABO的右边作等边△ABC,如图所示,求点O与点C的距离.
已知Rt△ABO中,AB=OB=2,∠ABO=90°.以AB为边,在Rt△ABO的右边作等边△ABC,如图所示,求点O与点C的距离.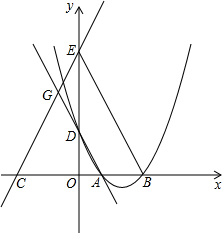 已知抛物线y=x2-(k+2)x+
已知抛物线y=x2-(k+2)x+ 图中表示的不等式的解集是
图中表示的不等式的解集是