题目内容
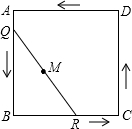 如图,正方形ABCD的边长为2,将长为2的线段QR的两端放在正方形的相邻的两边上同时滑动.如果点Q从点A出发,沿图中所示方向按A→B→C→D→A滑动到A止,同时点R从点B出发,沿图中所示方向按B→C→D→A→B滑动到B止.点N是正方形ABCD内任一点,把N点落在线段QR的中点M所经过的路线围成的图形内的概率记为P,则P=( )
如图,正方形ABCD的边长为2,将长为2的线段QR的两端放在正方形的相邻的两边上同时滑动.如果点Q从点A出发,沿图中所示方向按A→B→C→D→A滑动到A止,同时点R从点B出发,沿图中所示方向按B→C→D→A→B滑动到B止.点N是正方形ABCD内任一点,把N点落在线段QR的中点M所经过的路线围成的图形内的概率记为P,则P=( )A、
| ||
B、
| ||
C、
| ||
D、
|
考点:轨迹,几何概率
专题:
分析:根据直角三角形的性质,斜边上的中线等于斜边的一半,可知:点M到正方形各顶点的距离都为1,故点M所走的运动轨迹为以正方形各顶点为圆心,以1为半径的四个扇形,点M所经过的路线围成的图形的面积为正方形ABCD的面积减去4个扇形的面积,进而利用概率公式求出即可.
解答:解:根据题意得点M到正方形各顶点的距离都为1,点M所走的运动轨迹为以正方形各顶点为圆心,以1为半径的四个扇形,
∴点M所经过的路线围成的图形的面积为正方形ABCD的面积减去4个扇形的面积.
而正方形ABCD的面积为2×2=4,4个扇形的面积为4×
=π,
∴点M所经过的路线围成的图形的面积为4-π,
∴把N点落在线段QR的中点M所经过的路线围成的图形内的概率记为P,则P=
.
故选:A.
∴点M所经过的路线围成的图形的面积为正方形ABCD的面积减去4个扇形的面积.
而正方形ABCD的面积为2×2=4,4个扇形的面积为4×
| 90π×12 |
| 360 |
∴点M所经过的路线围成的图形的面积为4-π,
∴把N点落在线段QR的中点M所经过的路线围成的图形内的概率记为P,则P=
| 4-π |
| 4 |
故选:A.
点评:本题主要考查了点的轨迹以及直角三角形斜边上的中线等于斜边的一半,正方形的性质以及扇形面积的计算,得出点M所经过的路线围成的图形的面积是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,下列判断正确的是( )
如图,下列判断正确的是( )| A、∠2与∠4是同位角 |
| B、∠2与∠5是对顶角 |
| C、∠3与∠6是同位角 |
| D、∠5与∠3是内错角 |
下列运算正确的是( )
A、
| |||||||
B、
| |||||||
C、
| |||||||
D、|
|
已知关于x的不等式组
无解,则m取值范围是( )
|
| A、m<2 | B、m≤2 |
| C、m>2 | D、m≥2 |
如果(am•b•bn)3=a6b15,那么m,n的值分别是( )
| A、2,4 | B、2,5 |
| C、3,5 | D、3,-5 |
如果点P(5,y)在第四象限,则y的取值范围是( )
| A、y<0 |
| B、y>0 |
| C、y大于或等于0 |
| D、y小于或等于0 |
 如图5,A为反比例函数y=
如图5,A为反比例函数y=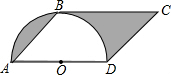 如图,已知?ABCD中,∠A=45°,AD=4cm,以AD为直径的半圆O与BC相切于点B,则图中阴影部分的面积是
如图,已知?ABCD中,∠A=45°,AD=4cm,以AD为直径的半圆O与BC相切于点B,则图中阴影部分的面积是