Question

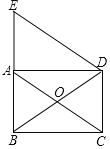
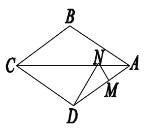
【题目】在菱形ABCD中，M是AD的中点，AB＝4，N是对角线AC上一动点，△DMN 的周长最小是2+，则BD的长为___________．

Answer 1

【答案】4

【解析】

根据题意，当B、N、M三点在同一条直线时，△DMN的周长最小为：BM+DM=2+，由DM=，则BM=，利用勾股定理的逆定理，得到∠AMB=90°，则得到△ABD为等边三角形，即可得到BD的长度.

解：如图：连接BD，BM，则AC垂直平分BD，则BN=DN，

当B、N、M三点在同一条直线时，△DMN的周长最小为：BM+DM=2+，

∵AD=AB=4，M是AD的中点，

∴AM=DM=，

∴BM=，

∵，

∴△ABM是直角三角形，即∠AMB=90°；

∵BM是△ABD的中线，

∴△ABD是等边三角形，

∴BD=AB=AD=4.

故答案为：4.