题目内容
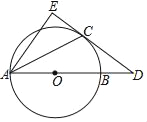
【题目】如图,![]() 中,
中,![]() ,
,![]() ,若点
,若点![]() 为射线
为射线![]() 上一动点,连接
上一动点,连接![]() ,将线段AE绕着点
,将线段AE绕着点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() .
.
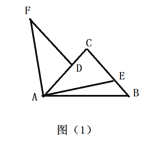
(1)如图![]() ,当点
,当点![]() 在线段
在线段![]() 上运动时;
上运动时;
①若![]() ,则
,则![]() _______ (直接写出答案);
_______ (直接写出答案);
②过![]() 点作
点作![]() 交
交![]() 于
于![]() 点,求证:
点,求证:![]() ;
;
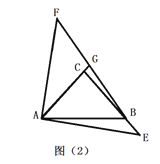
(2)当![]() 点在射线
点在射线![]() 上,(如图2) 连接
上,(如图2) 连接![]() 与直线
与直线![]() 交于
交于![]() 点,若
点,若![]() ,求
,求![]() 的值.
的值.
【答案】(1)①60°;②见解析;(2)![]() 或
或![]()
【解析】
(1)①由旋转的性质可得∠EAF=90°,再根据角的和差求出∠CAE的度数,然后根据∠FAC=∠EAF-∠CAE计算即可;
②通过证明形△ADF≌△EAC得到:AD=CE,FD=AC,再利用等量代换即可证明结论成立;
(2)分两种情况求解:①当点E在线段CB的延长线上时,过F作FD⊥AG的延长线交于点D,易证![]() ,由(1)可知△ADF≌△ECA,△GDF≌△GCB,可得CG=GD,AD=CE,即可求得
,由(1)可知△ADF≌△ECA,△GDF≌△GCB,可得CG=GD,AD=CE,即可求得![]() 的值,即可解题;②当点E在线段CB的上时.过F作FD⊥AG点D,与①同理即可求解.
的值,即可解题;②当点E在线段CB的上时.过F作FD⊥AG点D,与①同理即可求解.
证明:(1)①由旋转的性质得∠EAF=90°,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴∠FAC=90°-30°=60°;
②∵∠FAD+∠CAE=90°,∠FAD+∠AFD =90°,
∴∠CAE=∠AFD,
在△ADF和△ECA中,
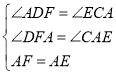 ,
,
∴△ADF≌△ECA(AAS),
∴AD=EC,FD=AC,
∴CE+CD=AD+CD=AC=FD,即EC+CD=DF;
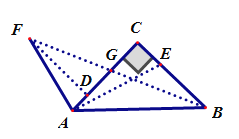
(2)①当点E在线段CB的延长线上时,过F作FD⊥AC的延长线交于点D,如图2,

∵![]() ,BC=AC,CE=CB+BE,
,BC=AC,CE=CB+BE,
∴![]() ,
,
由(1)知:△ADF≌△ECA,
∴AD=CE,DF=AC,
∴![]() ,
,
∴![]() ,
,
∵AC=BC,DF=AC,
∴DF=BC,
又∵∠FGD=∠BGC,∠D=∠BCG=90°,
∴△GDF≌△GCB,
∴DG=CG,
∴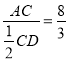 ,
,
∴![]() ;
;
②当点E在线段CB的上时,过F作FD⊥AC于点D,如图3,
∵![]() , BC=CE+BE,
, BC=CE+BE,
∴![]() ,
,
∵BC=AC,
∴![]() ,
,
由(1)知:△ADF≌△ECA,
∴AD=CE,DF=AC,
∴![]() ,
,
∴![]() ,
,
∵AC=BC,DF=AC,
∴DF=BC,
又∵∠FGD=∠BGC,∠ADF=∠BCG=90°,
∴△GDF≌△GCB,
∴DG=CG,
∴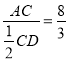 ,
,
∴![]() .
.
综上可知,![]() 的值是
的值是![]() 或
或![]() .
.
故答案为:![]() 或
或![]() .
.

 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案