Question

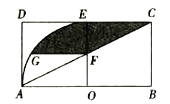
【题目】如图所示，矩形中，，点分别是边的中点，的圆心是点与相交于点交于点，则图中阴影部分的面积为__________．

Answer 1

【答案】

【解析】

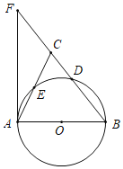
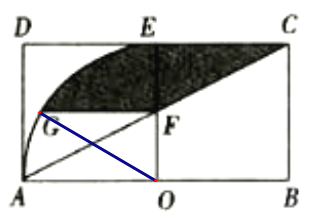
连接OG，根据矩形的性质、中点的定义、中位线的性质可得OE⊥DC、OE⊥AB，AO=2、EC=2、EF=1、OF=1然后求得S△EFC；然后再根据含30°的直角三角形的性质和勾股定理求得FG=、∠FOG=60°，运用扇形的面积公式可求S扇形OGE；然后根据S阴影FEG= S扇形OGE –S△FOG求得S阴影FEG的面积，最后根据S阴影= S阴影FEG+ S△EFC计算即可．

解：连接OG，

∵矩形中，

∴AB//CD，AB=CD=4，AD//BC，AD=BC=2，

∵点分别是边的中点

∴OE⊥DC，OE⊥AB，OE//AD,AO=OB=AB=2,EC=DE=CD=2,

∴EF//DA

∴EF=AD=1,

∴OF=OE-EF=1

∴S△EFC==1

∵在Rt△OFG中，OG=OA=2，OF=1

∴∠OGF=30°，FG=

∴∠FOG=60°

∴S阴影FEG= S扇形OGE –S△FOG=

∴S阴影= S阴影FEG+ S△EFC=．

故答案为．