题目内容
4.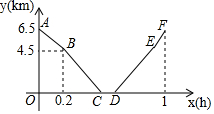 从甲地到乙地,先是一段上坡路,然后是一段平路,小明骑车从甲地出发,到达乙地后休息一段时间,然后原路返回甲地.假设小明骑车在上坡、平路、下坡时分别保持匀速前进,已知小明骑车上坡的速度比平路上的速度每小时少5km,下坡的速度比在平路上的速度每小时多5km,设小明出发xh后,到达离乙地ykm的地方,图中的折线ABCDEF表示y与x之间的函数关系.其中正确的个数为( )
从甲地到乙地,先是一段上坡路,然后是一段平路,小明骑车从甲地出发,到达乙地后休息一段时间,然后原路返回甲地.假设小明骑车在上坡、平路、下坡时分别保持匀速前进,已知小明骑车上坡的速度比平路上的速度每小时少5km,下坡的速度比在平路上的速度每小时多5km,设小明出发xh后,到达离乙地ykm的地方,图中的折线ABCDEF表示y与x之间的函数关系.其中正确的个数为( )(1)小明骑车在平路上的速度为15km/h,小明下坡的速度为20km/h
(2)小明在乙地休息了0.1h.
(3)线段AB函数关系式y=-10x+6.5(0≤x≤0.2),EF所对应的函数关系式y=20x-13.5(0.9≤x≤1)
(4)从甲地到乙地经过丙地,如果小明两次经过丙地的时间间隔为0.85h,丙地与甲地之间的路程为1千米.
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 (1)先计算出小明骑车上坡的速度,再根据骑车上坡的速度比平路上的速度每小时少5km求出小明平路上的速度;
(2)求出小明下坡的速度,平路上所用的时间,下坡所用的时间,那么小明在乙地休息的时间=1h-小明上坡所用的时间0.2h-平路上所用的时间-下坡所用的时间;
(3)根据上坡的速度为10km/h,下坡的速度为20km/h,所以线段AB所对应的函数关系式为:yAB=6.5-10x,线段EF所对应的函数关系式为yEF=4.5+20(x-0.9),即可解答;
(4)设小明出发a小时第一次经过丙地,根据题意得到6.5-10a=20(a+0.85)-13.5,即可求出丙地与甲地之间的路程.
解答 解:(1)小明骑车上坡的速度为:(6.5-4.5)÷0.2=10(km/h),
平路上的速度为:10+5=15(km/h),
(2)下坡的速度为:15+5=20(km/h),
平路上所用的时间为:2(4.5÷15)=0.6h,
下坡所用的时间为:(6.5-4.5)÷20=0.1h
所以小明在乙地休息了:1-0.1-0.6-0.2=0.1(h).
(3)由题意可知:上坡的速度为10km/h,下坡的速度为20km/h,
所以线段AB所对应的函数关系式为:y=6.5-10x,
即yAB=-10x+6.5(0≤x≤0.2).
线段EF所对应的函数关系式为yEF=4.5+20(x-0.9).
即yEF=20x-13.5(0.9≤x≤1);
(4)由题意可知:小明第一次经过丙地在AB段,第二次经过丙地在EF段,
设小明出发a小时第一次经过丙地,则小明出发后(a+0.85)小时第二次经过丙地,
6.5-10a=20(a+0.85)-13.5,
解得:a=0.1.0.1×10=1(千米).
所以丙地与甲地之间的距离为1千米.
综上可知其中正确的个数为4个,
故选D.
点评 本题考查了一次函数的应用,行程问题数量关系的运用,一次函数解析式的确定,一元一次方程的运用.解决本题的关键是读懂函数图象,求出一次函数的解析式.

 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案| A. | m3•m2 | B. | (m3)2 | C. | m12÷m2 | D. | m6•m |
| A. | $\frac{AD}{DE}$=$\frac{DB}{EC}$ | B. | $\frac{AD}{AE}$=$\frac{EC}{BD}$ | C. | $\frac{AE}{AC}$=$\frac{AD}{AB}$ | D. | $\frac{AD}{EC}$=$\frac{AC}{BC}$ |
| A. | $\frac{5}{2}$a元 | B. | $\frac{5}{3}$a元 | C. | 40%a元 | D. | 60%a元 |
| A. |  | B. |  | C. |  | D. |  |
| A. | 某市“明天降雨的概率是75%”表示明天有5%的时间会降雨 | |
| B. | 随机抛掷一枚均匀的硬币,落地后正面一定朝上 | |
| C. | 在一次抽奖活动中,“中奖的概率是$\frac{1}{100}$”表示抽奖100次就一定会中奖 | |
| D. | 在同一年出的367名学生中,至少有两人的生日是同一天 |
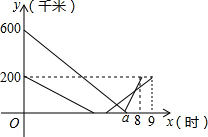 甲、乙两车在连通A、B、C三地的公路上行驶,B地在A地、C地之间,甲车从A地出发匀速向C地行驶,同时乙车从C地出发匀速向B地行驶,到达B地并在B地停留1小时后,按原路原速返回到C地.在两车行驶的过程中,甲、乙两车距B地的路程y(千米)与行驶时间x(小时)之间的函数图象如图所示.下列说法:
甲、乙两车在连通A、B、C三地的公路上行驶,B地在A地、C地之间,甲车从A地出发匀速向C地行驶,同时乙车从C地出发匀速向B地行驶,到达B地并在B地停留1小时后,按原路原速返回到C地.在两车行驶的过程中,甲、乙两车距B地的路程y(千米)与行驶时间x(小时)之间的函数图象如图所示.下列说法: