��Ŀ����
����Ŀ���Ѽ���ͼ��ƴ��һ���µ�ͼ�Σ���ͨ��ͼ������ļ��㣬�������Եõ�һЩ���õ�ʽ�ӣ���������һЩ������ͼ�ε������
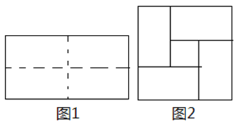
��1��ѡ���⣺ͼ1��һ����2a����2b��a��b���ij����Σ��ü�����ͼ�����ߣ��Գ��ᣩ�����������ֳ��Ŀ���״�ʹ�С��һ����С�����Σ�Ȼ��ͼ2����ƴ��һ�����м�յģ������Σ����м�յIJ�������ǣ��� ��
A��2ab B����a+b��2 C����a��b��2 D��a2��b2
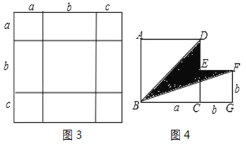
��2����ͼ3���ǽ�����������ȵ�С��������С������ƴ��һ���߳�Ϊa+b+c�������Σ����ò�ͬ�ķ����������ͼ�ε�������ݴˣ����ܷ���ʲô���ۣ���ֱ��д��������
��3����ͼ4���ǽ������߳��ֱ�Ϊa��b��������ƴ��һ��B��C��G������ͬһֱ���ϣ�����BD��BF�������������εı߳�����a+b=10��ab=20������Ӱ���ֵ������
���𰸡���1��C����2����a+b+c��2=a2+b2+c2+2ab+2bc+2ac����3��20
��������
��1����ͼ2��֪�м�С�����εı߳�Ϊ(![]() )��������ô𰸣�
)��������ô𰸣�
��2��һ�ֿ�����3�������ε������6�����ε������һ���Ǵ������ε�������ɵõ�ʽ��
��3������S��Ӱ=������ABCD�����+������ECGF�����-![]() BGF�����-
BGF�����-![]() ABD�������⼴�ɣ�
ABD�������⼴�ɣ�
(1) ��ͼ2��֪�м�С�����εı߳�Ϊ(![]() )��
)��
���м�յIJ�������ǣ�![]() ��
��
�ʴ�Ϊ��C��
(2)��ͼ��3�������ε������6�����ε������Ϊ��![]() ��
��
������������![]() ��
��
��![]()

(3)��![]() ��
��![]() ��
��
��![]()
![]()
![]()
![]()
![]()
![]()
![]() ��
��