Question

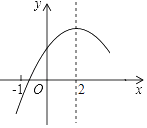
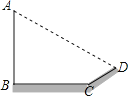
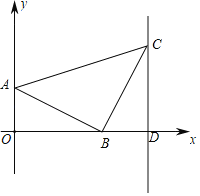
【题目】如图平面直角坐标系中，A点坐标为（0，1），AB＝BC＝，∠ABC＝90°，CD⊥x轴．

（1）填空：B点坐标为　 　，C点坐标为　 　．

（2）若点P是直线CD上第一象限上一点且△PAB的面积为6.5，求P点的坐标；

（3）在（2）的条件下点M是x轴上线段OD之间的一动点，当△PAM为等腰三角形时，直接写出点M的坐标．

Answer 1

【答案】（1）（3，0），（4，3）；（2）P（4，4）；（3）（1，0）或（）．

【解析】

（1）根据勾股定理可求出OB＝3，证明△AOB≌△DBC，可得出OA＝BD＝1，OB＝DC＝3，则B，C两点的坐标可求出；

（2）设P（4，a），由三角形面积可得出关于a的方程，解方程即可得出答案；

（3）根据M是x轴上线段OD之间的一动点，画出图形，有两种可能，当AP＝MP或AM＝MP时，设M（x，0），可得出关于x的方程，解方程即可得解．

解：（1）∵A点坐标为（0，1），AB＝BC＝，

∴OB＝＝＝3，

∵∠ABC＝90°，∠AOB＝90°，

∴∠OAB+∠ABO＝90°，∠ABO+∠CBD＝90°，

∴∠OAB＝∠CBD，

∵∠AOB＝∠BDC，

∴△AOB≌△DBC（AAS），

∴OA＝BD＝1，OB＝DC＝3，

∴B（3，0），C（4，3），

故答案为：（3，0），（4，3）；

（2）如图1，设P（4，a），

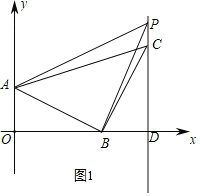
∵△PAB的面积为6.5，

∴S△PAB＝S四边形AODP﹣S△AOB﹣S△BDP＝＝6.5，

解得：a＝4，

∴P（4，4）；

（3）M是x轴上线段OD之间的一动点，如图2，当AP＝MP，

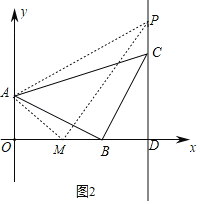
∵P（4，4），A（0，1），设M（x，0），

∴42+（4﹣1）2＝（x﹣4）2+42，

解得：x1＝1，x2＝7（舍去），

∴M（1，0），

如图3，AM＝MP时，

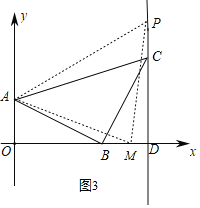
x2+12＝（x﹣4）2+42，

解得x＝，

∴，

综合以上可得点M的坐标为（1，0）或（）．