题目内容
 如图,△ABC边长分别为AB=14,BC=16,AC=26,P为∠A的平分线AD上一点,且BP⊥AD,M为BC的中点,则PM的值是
如图,△ABC边长分别为AB=14,BC=16,AC=26,P为∠A的平分线AD上一点,且BP⊥AD,M为BC的中点,则PM的值是考点:三角形中位线定理,等腰三角形的判定与性质
专题:
分析:延长BP交AC于点E,首先证明△APB≌△APE,可得AB=AE=14,PE=PB,进而得到EC=12,再根据三角形中位线定理可以计算出PM=
EC=6.
| 1 |
| 2 |
解答:解:延长BP交AC于点E,
∵AD为∠BAC的平分线,
∴∠BAP=∠EAP,
∵BP⊥AD于D,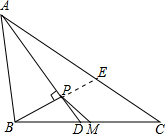
∴∠APB=∠APE=90°,
在△APB和△APE中,
,
∴△APB≌△APE(ASA),
∴AB=AE=14,
∵AC=26,
∴EC=26-14=12,
∵△APB≌△APE,
∴BP=EP,
∵M是BC的中点,
∴PM=
EC=
×12=6.
故答案为6.
∵AD为∠BAC的平分线,
∴∠BAP=∠EAP,
∵BP⊥AD于D,

∴∠APB=∠APE=90°,
在△APB和△APE中,
|
∴△APB≌△APE(ASA),
∴AB=AE=14,
∵AC=26,
∴EC=26-14=12,
∵△APB≌△APE,
∴BP=EP,
∵M是BC的中点,
∴PM=
| 1 |
| 2 |
| 1 |
| 2 |
故答案为6.
点评:此题主要考查了全等三角形的判定与性质,以及三角形中位线定理,关键是证明出△APB≌△APE,得到AB=AE=14,PE=PB.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
观察下列图形:
它们是按一定规律排列的,依照此规律,第9个图形中共有★( )

它们是按一定规律排列的,依照此规律,第9个图形中共有★( )

| A、16个 | B、18个 |
| C、20个 | D、24个 |
 如图,四边形OBCD中,∠BCD=90°,E为CD的中点,以OB为半径的⊙O切CD于E,交BC于M,若BM=CM=2,则OC的长为( )
如图,四边形OBCD中,∠BCD=90°,E为CD的中点,以OB为半径的⊙O切CD于E,交BC于M,若BM=CM=2,则OC的长为( ) 如图,在△ABC与△AEF中,∠AFE=90°,AB=
如图,在△ABC与△AEF中,∠AFE=90°,AB=