Question

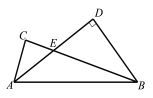
【题目】如图，ABCD的对角线AC、BD相交于点O，AB⊥AC，AB＝3，BC＝5，点P从点A出发，沿AD以每秒1个单位的速度向终点D运动．连结PO并延长交BC于点Q．设点P的运动时间为t秒．

（1）求BQ的长，（用含t的代数式表示）

（2）当四边形ABQP是平行四边形时，求t的值

（3）当点O在线段AP的垂直平分线上时，直接写出t的值．

Answer 1

【答案】（1）BQ＝5﹣t;（2）秒;（3）t＝.

【解析】

（1）利用平行四边形的性质可证△APO≌△CQO，则AP＝CQ，再利用即可得出答案；

（2）由平行四边形性质可知AP∥BQ，当AP＝BQ时，四边形ABQP是平行四边形，建立一个关于t的方程，解方程即可求出t的值；

（3）在Rt△ABC中，由勾股定理求出AC的长度，进而求出AO的长度，然后利用的面积求出EF的长度，进而求出OE的长度，而AE可以用含t的代数式表示出来，最后在中利用勾股定理即可求值.

解：（1）∵四边形ABCD是平行四边形，

∴OA＝OC，AD∥BC，

∴∠PAO＝∠QCO，

∵∠AOP＝∠COQ，

∴△APO≌△CQO（ASA），

∴AP＝CQ＝t，

∵BC＝5，

∴BQ＝BC-CQ=5﹣t；

（2）∵AP∥BQ，

当AP＝BQ时，四边形ABQP是平行四边形，

即t＝5﹣t，

t＝ ，

∴当t为秒时，四边形ABQP是平行四边形；

（3）t＝ ，

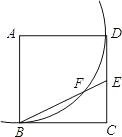
如图，

在Rt△ABC中，

∵AB＝3，BC＝5，

∴AC=

∴AO＝CO＝AC＝2，

∴3×4＝5×EF，

∴，

∴，

∵OE是AP的垂直平分线，

∴AE＝AP＝t，∠AEO＝90°，

由勾股定理得：AE2+OE2＝AO2，

或（舍去）

∴当秒时，点O在线段AP的垂直平分线上．