题目内容
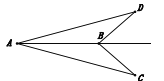
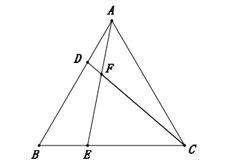
【题目】如图,在等边![]() 中,点
中,点![]() 分别在边
分别在边![]() 上,
上,![]() ,线段
,线段![]() 交于点
交于点![]()
![]() 求证:
求证:![]()
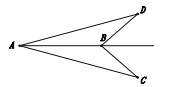
![]() 连接
连接![]() ,当
,当![]() 时,求证:
时,求证:![]() .
.
【答案】(1)详见解析;(2)详见解析.
【解析】
(1)证明△ABE△CAD即可;
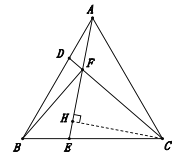
(2)过点C作CH⊥AE,垂足为H,通过证明△BFC△CHA,得到CF=AH,再证明∠FCH=30°,由30°角所对直角边等于斜边的一半,得到CF=2FH,进而可以得到AF=FH,即可得到结论.
(1)∵△ABC等边三角形ABC中,∴∠B=∠BCA=∠CAB=60°,AB=CA=BC.
在△ABE和△CAD中,∵BE=AD,∠B=∠CAB,AB=CA,∴△ABE△CAD,∴AE=CD;
(2)过点C作CH⊥AE,垂足为H,∴∠CHA=90°,∴∠BFC=90°,∠BFC=∠CHA.
∵△ABE△CAD,∴∠BAE=∠ACD.
∵∠CAB-∠BAE=∠BCA-∠ACD,即∠CAE=∠BCD.
在△BFC和△CHA中,∵∠BFC=∠CHA,∠BCD=∠CAE,BC=CA,∴△BFC△CHA,∴CF=AH.
∵∠CFE=∠CAE+∠ACD =∠CAE+∠BAE=∠CAB=60°.
∴∠FCH=180°-∠CHA-∠CFE =180°-90°-60°=30°,∴CF=2FH,∴AH=2FH,即AF+FH=2FH,∴AF=FH,∴CF=2AF.

练习册系列答案
相关题目