题目内容
阅读以下的例题求解:例:已知x>0,求函数y=x+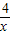 的最小值.
的最小值.解:令a=x,b=
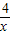 ,则有a+b≥2
,则有a+b≥2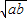 ,得y=x+
,得y=x+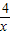 ≥2
≥2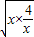 =4,当且仅当x=
=4,当且仅当x=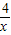 时,即x=2时,函数有最小值,最小值为4.
时,即x=2时,函数有最小值,最小值为4.根据上面回答下列问题:
①已知x>0,则当x=______
【答案】分析:①根据例题,可得y=2x+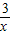 ≥2
≥2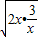 =2
=2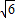 ,当且仅当2x=
,当且仅当2x=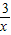 时,函数y=2x+
时,函数y=2x+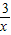 取到最小值,最小值为2
取到最小值,最小值为2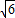 ;
;
②首先设这个矩形的长为xm,篱笆周长是ym,可得函数解析式为:y=2(x+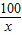 ),根据例题,即可求得答案;
),根据例题,即可求得答案;
③原函数可变形为:y=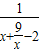 ,由x+
,由x+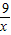 有最小值,即可求得自变量x取何值时,函数
有最小值,即可求得自变量x取何值时,函数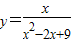 取到最大值,并求得最大值.
取到最大值,并求得最大值.
解答:解:①∵令a=2x,b=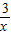 ,则有a+b≥2
,则有a+b≥2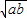 ,
,
∴y=2x+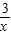 ≥2
≥2 =2
=2 ,当且仅当2x=
,当且仅当2x=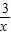 时,取等号,
时,取等号,
∴x=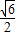 时,函数有最小值,最小值为2
时,函数有最小值,最小值为2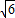 .
.
故答案为: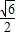 ,2
,2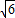 ;
;
②设这个矩形的长为xm,篱笆周长是ym,
∵面积为100m2,
∴宽为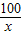 m,
m,
∴y=2(x+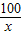 )≥4
)≥4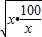 =40,当且仅当x=
=40,当且仅当x=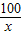 时,即x=10时,函数有最小值,最小值为40,
时,即x=10时,函数有最小值,最小值为40,
∴这个矩形的长为10m、宽为10m时,所用的篱笆最短,最短的篱笆周长是40m.
③∵y=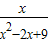 =
=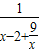 =
=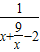 ,
,
又∵x+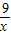 ≥2
≥2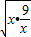 =6,当且仅当x=
=6,当且仅当x=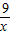 时,x+
时,x+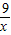 有最小值,
有最小值,
∵x>0,
∴当x=3时,x+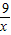 有最小值,最小值为6,
有最小值,最小值为6,
∴此时y有最大值,最大值为:y=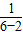 =
= ;
;
∴当x=3时,函数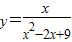 取到最大值,最大值为
取到最大值,最大值为 .
.
点评:此题考查了几何不等式的应用.此题难度较大,解题的关键是理解例题,并能借助于例题求解.
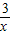 ≥2
≥2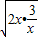 =2
=2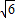 ,当且仅当2x=
,当且仅当2x=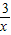 时,函数y=2x+
时,函数y=2x+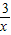 取到最小值,最小值为2
取到最小值,最小值为2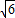 ;
;②首先设这个矩形的长为xm,篱笆周长是ym,可得函数解析式为:y=2(x+
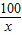 ),根据例题,即可求得答案;
),根据例题,即可求得答案;③原函数可变形为:y=
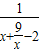 ,由x+
,由x+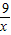 有最小值,即可求得自变量x取何值时,函数
有最小值,即可求得自变量x取何值时,函数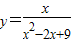 取到最大值,并求得最大值.
取到最大值,并求得最大值.解答:解:①∵令a=2x,b=
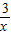 ,则有a+b≥2
,则有a+b≥2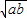 ,
,∴y=2x+
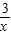 ≥2
≥2 =2
=2 ,当且仅当2x=
,当且仅当2x=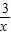 时,取等号,
时,取等号,∴x=
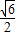 时,函数有最小值,最小值为2
时,函数有最小值,最小值为2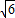 .
.故答案为:
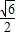 ,2
,2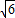 ;
;②设这个矩形的长为xm,篱笆周长是ym,
∵面积为100m2,
∴宽为
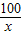 m,
m,∴y=2(x+
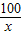 )≥4
)≥4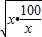 =40,当且仅当x=
=40,当且仅当x=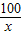 时,即x=10时,函数有最小值,最小值为40,
时,即x=10时,函数有最小值,最小值为40,∴这个矩形的长为10m、宽为10m时,所用的篱笆最短,最短的篱笆周长是40m.
③∵y=
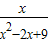 =
=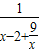 =
=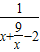 ,
,又∵x+
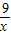 ≥2
≥2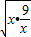 =6,当且仅当x=
=6,当且仅当x=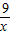 时,x+
时,x+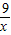 有最小值,
有最小值,∵x>0,
∴当x=3时,x+
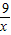 有最小值,最小值为6,
有最小值,最小值为6,∴此时y有最大值,最大值为:y=
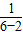 =
= ;
;∴当x=3时,函数
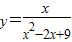 取到最大值,最大值为
取到最大值,最大值为 .
.点评:此题考查了几何不等式的应用.此题难度较大,解题的关键是理解例题,并能借助于例题求解.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
 的最小值.
的最小值. ,得y=x+
,得y=x+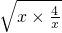 =4,当且仅当x=
=4,当且仅当x= 取到最小值,最小值为______;
取到最小值,最小值为______;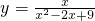 取到最大值,最大值为多少?
取到最大值,最大值为多少?