题目内容
14.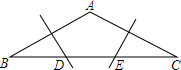 已知:如图,在△ABC中,AB=AC,∠A=120°,AB、AC的垂直平分线分交DE于点D、E.若BC=21cm,则DE=7cm.
已知:如图,在△ABC中,AB=AC,∠A=120°,AB、AC的垂直平分线分交DE于点D、E.若BC=21cm,则DE=7cm.
分析 根据等腰三角形两底角相等求出∠B=30°,再根据直角三角形30°角所对的直角边等于斜边的一半可得BD=2DE,然后利用勾股定理列式求出BE,再求出AB,即可得解.
解答 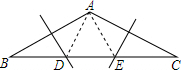 解:∵AB=AC,∠A=120°
解:∵AB=AC,∠A=120°
∴∠B=∠c=$\frac{1}{2}$(180°-∠A)=$\frac{1}{2}$(180°-120°)=30°,
∵AB、AC的垂直平分线分交DE于点D、E,
∴AD=BD,AE=CE,
∴∠BAD=∠B=30°,∠CAE=∠C=30°,
∴∠ADE=∠AED=60°,
∴△ADE是等边三角形,
∴DE=$\frac{1}{3}$BC=$\frac{1}{3}×$21=7cm.
故答案为:7.
点评 本题考查了线段垂直平分线的定义,等腰三角形的性质,勾股定理的应用,以及直角三角形30°角所对的直角边等于斜边的一半的性质,熟记性质是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2.给出下列各数:①4;②$\sqrt{4}$;③$\sqrt{40}$;④$\sqrt{40}$+1.其中,二次根式有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
 如图,在?ABCD中,AC=2,∠ADB=90°,∠BCD=45°,求BD的长.
如图,在?ABCD中,AC=2,∠ADB=90°,∠BCD=45°,求BD的长.