Question

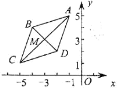
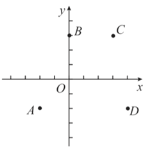
【题目】如图，在平面直角坐标系中，点，y是关于的二次函数，抛物线经过点.抛物线经过点抛物线经过点抛物线经过点则下列判断：

①四条抛物线的开口方向均向下；

②当时，四条抛物线表达式中的均随的增大而增大；

③抛物线的顶点在抛物线顶点的上方；

④抛物线与轴交点在点的上方.

其中正确的是

A.①②④B.①③④

C.①②③D.②③④

Answer 1

【答案】A

【解析】

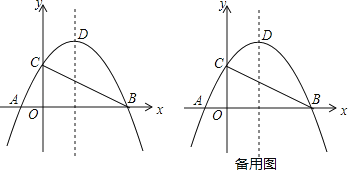
根据BC的对称轴是直线x=1.5,的对称轴是直线x=1，画大致示意图，即可进行判定.

解：①由可知，四条抛物线的开口方向均向下，

故①正确；

②和的对称轴是直线x=1.5,和的对称轴是直线x=1,开口方向均向下,所以当时，四条抛物线表达式中的均随的增大而增大，

故②正确；

③和的对称轴都是直线x=1.5，D关于直线x=1.5的对称点为(-1,-2)，而A点坐标为(-2,-2),可以判断比更陡，所以抛物线的顶点在抛物线顶点的下方，

故③错误；

④的对称轴是直线x=1, C关于直线x=1的对称点为(-1,3)，可以判断出抛物线与轴交点在点的上方，

故④正确.

故选：A.