题目内容
17.(1)如图1,锐角△ABC中,分别以AB、AC为边向外作等边△ABD和等边△ACE,连结BE、CD,试猜想BE与CD的大小关系,并证明你的结论;(2)如图2,四边形ABCD中,AB=4,BC=3,AD=CD,∠ABC=30°,∠ADC=60°,求BD的长;
(3)如图3,四边形ABCD中,AB=4,BC=3,∠ABC=∠ACD=∠ADC=45°,求BD的长.
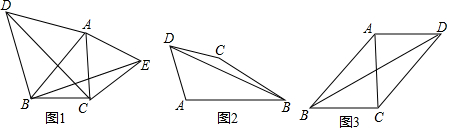
分析 (1)根据等边三角形性质得出AD=AB,AC=AE,∠DAB=∠EAC=60°,求出∠DAC=∠BAE,根据SAS推出△DAC≌△BAE即可;
(2)利用∠ADC=60°,AD=DC可把△ADB绕点D逆时针旋转60°得到△DCE,如图2,根据旋转的性质可判断△DBE为等边三角形,得到BD=BE,接着利用∠ABC=30°可得到Rt△BCE,然后利用勾股定理计算出BE,从而得到BD的长.
(3)如图3,在△ABC的外部,以A为直角顶点作等腰直角△BAE,使∠BAE=90°,AE=AB,连接EA、EB、EC,证明△EAC≌△BAD,证明BD=CE,然后在直角三角形BCE中利用勾股定理即可求解.
解答 解:(1)CD=EB,
理由是:∵△ABD和△ACE是等边三角形,
∴AD=AB,AC=AE,∠DAB=∠EAC=60°,
∴∠DAB+∠BAC=∠EAC+∠BAC,
∴∠DAC=∠BAE,
在△DAC和△BAE中,
$\left\{\begin{array}{l}{AD=AB}\\{∠DAC=∠BAE}\\{AC=AE}\end{array}\right.$,
∴△DAC≌△BAE(SAS),
∴CD=EB;
(2)∵∠ADC=60°,AD=DC,
∴把△ADB绕点D逆时针旋转60°得到△DCE,如图2,连接BE,
∴DB=DE,CE=AB=4,∠DEC=∠DBA,∠BDE=60°,
∴△DBE为等边三角形,
∴BD=BE,∠DBE=∠DEB=60°,
即∠DEC+∠CEB+∠CBE+∠CBD=120°,
∵∠ABC=30°,
∴∠DBA+∠CBD=30°,
∴∠CBE+∠CEB=90°,
∴∠BCE=90°,
在Rt△BCE中,BE=$\sqrt{B{C}^{2}+C{E}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∴BD的长为5;
(3)如图2,在△ABC的外部,以A为直角顶点作等腰直角△BAE,使∠BAE=90°,AE=AB,连接EA、EB、EC,
∵∠ACD=∠ADC=45°,
∴AC=AD,∠CAD=90°,
∴∠BAE+∠BAC=∠CAD+∠BAC,即∠EAC=∠BAD,
在△EAC和△BAD中,
$\left\{\begin{array}{l}{AE=AB}\\{∠EAC=∠BAD}\\{AC=AD}\end{array}\right.$,
∴△EAC≌△BAD(SAS),
∴BD=CE.
∵AE=AB=4,
∴BE=$\sqrt{{4}^{2}+{4}^{2}}$=4$\sqrt{2}$,∠ABE=45°,
∵∠ABC=45°,
∴∠ABC+∠ABE=45°+45°=90°,
∴EC=$\sqrt{(4\sqrt{2})^{2}+{3}^{2}}$=$\sqrt{41}$,
∴BD=CE=$\sqrt{41}$.
点评 本题是三角形的综合题,难度适中,考查了全等三角形的性质和判定,等边三角形的性质和应用,等腰直角三角形的性质和判定,旋转的性质和勾股定理,全等三角形的判定结合全等三角形的性质是证明线段相等或角相等的工具,注意:全等三角形的对应边相等,对应角相等,全等三角形的判定定理有SAS,ASA,AAS,SSS.

 初中学业考试导与练系列答案
初中学业考试导与练系列答案 如图所示,下列说法错误的是( )
如图所示,下列说法错误的是( )| A. | ∠A和∠B是同旁内角 | B. | ∠A和∠3是内错角 | ||
| C. | ∠1和∠3是内错角 | D. | ∠C和∠3是同位角 |
2004年1月至2012年6月执行的收费标准:
| 月用电量(度) | 50度有以下部分 | 超过50度但不超过200度部分 | 超过200度以上部分 |
| 单价(元/度) | 0.53 | 0.56 | 0.63 |
| 月用电量(度) | 230度有以下部分 | 超过230度但不超过400度部分 | 超过400度以上部分 |
| 单价(元/度) | 0.53 | 0.58 | 0.83 |
(2)若新政后小明家的月用电量为a度,请你用含a的代数式表示当月的电费支出.
| A. | 4x2+1 | B. | 4x2-2x+1 | C. | 4x2-4x-1 | D. | 4x2-4x+1 |
 如图,C是线段AB的中点,D是线段AC的中点,已知线段CD=3cm,则线段AB=cm12.
如图,C是线段AB的中点,D是线段AC的中点,已知线段CD=3cm,则线段AB=cm12.