题目内容
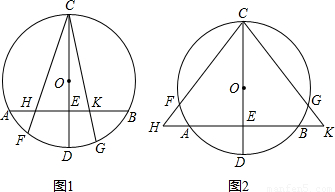
⊙O中,CD为直径,CD⊥AB,垂足为E.(1)如图1,以C为端点作两条射线,一条交⊙O、弦AB分别为F、H,另一条交⊙O、弦AB分别为G、K.求证:CF•CH=CG•CK.
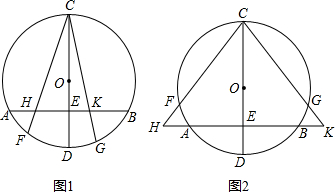
(2)如图2,若以C为端点的两条射线,一条交⊙O、直线AB分别为F、H,另一条交⊙O、直线AB分别为G、K.问结论CF•CH=CG•CK是否依然成立?若成立,请给出证明;若不成立,请说明理由.
分析:(1)连接DF,DG,由CD为⊙O的直径可以得到∠F=90°,又CD为直径,CD⊥AB,垂足为E得到∠AEH=90°,所以∠CEH=∠F,然后利用已知条件可以证明△HCE∽△DCF,接着利用相似三角形的性质得到
=
,变形为CF•CH=CE•CD.同理得到CG•CK=CE•CD,由此即可解决问题;
(2)成立.证明过程同(1).
| CH |
| CD |
| CE |
| CF |
(2)成立.证明过程同(1).
解答: (1)证明:连接DF,DG,
(1)证明:连接DF,DG,
∵CD为⊙O的直径,
∴∠F=90°,
又∵直径CD⊥弦AB,∴∠CEH=90°,
∴∠CEH=∠F.
又∵∠CEH=∠DCF,
∴△HCE∽△DCF,
∴
=
,
∴CF•CH=CE•CD.
同理:CG•CK=CE•CD,
∴CF•CH=CG•CK;
(2)解:连接DF,DG,
∵CD为⊙O的直径,
∴∠F=90°,
又∵直径CD⊥弦AB,∴∠CEH=90°,
∴∠CEH=∠F.
又∵∠CEH=∠DCF,
∴△HCE∽△DCF,
∴
=
,
∴CF•CH=CE•CD.
同理:CG•CK=CE•CD,
∴CF•CH=CG•CK.
 (1)证明:连接DF,DG,
(1)证明:连接DF,DG,∵CD为⊙O的直径,
∴∠F=90°,
又∵直径CD⊥弦AB,∴∠CEH=90°,
∴∠CEH=∠F.
又∵∠CEH=∠DCF,
∴△HCE∽△DCF,
∴
| CH |
| CD |
| CE |
| CF |
∴CF•CH=CE•CD.
同理:CG•CK=CE•CD,
∴CF•CH=CG•CK;
(2)解:连接DF,DG,
∵CD为⊙O的直径,
∴∠F=90°,
又∵直径CD⊥弦AB,∴∠CEH=90°,
∴∠CEH=∠F.
又∵∠CEH=∠DCF,
∴△HCE∽△DCF,
∴
| CH |
| CD |
| CE |
| CF |
∴CF•CH=CE•CD.
同理:CG•CK=CE•CD,
∴CF•CH=CG•CK.
点评:本题考查了在圆中证明等积式成立,此类题目证明的思路是将等积式转化为比例式,再找三角形,证明三角形相似即可.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
 3、已知在⊙O中,CD为直径,AB是弦,AB⊥CD于M,CD=15cm,若OM:OC=3:5,则AB=
3、已知在⊙O中,CD为直径,AB是弦,AB⊥CD于M,CD=15cm,若OM:OC=3:5,则AB=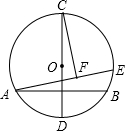 如图,半径为4的⊙O中,CD为直径,弦AB⊥CD且过半径OD的中点,点E为⊙O上一动点,CF⊥AE于点F.当点E从点B出发顺时针运动到点D时,点F所经过的路径长为( )
如图,半径为4的⊙O中,CD为直径,弦AB⊥CD且过半径OD的中点,点E为⊙O上一动点,CF⊥AE于点F.当点E从点B出发顺时针运动到点D时,点F所经过的路径长为( ) (1998•四川)已知:如图⊙O中,CD为直径,半径OA⊥CD,点B在OA上,延长CB交⊙O于点M,
(1998•四川)已知:如图⊙O中,CD为直径,半径OA⊥CD,点B在OA上,延长CB交⊙O于点M,