题目内容
3. 如图,在矩形ABCD中,BC=$\sqrt{2}$AB,∠ADC的平分线交边BC于点E,AH⊥DE于点H,连接CH并延长交边AB于点F,连接AE交CF于点O.给出下列命题:
如图,在矩形ABCD中,BC=$\sqrt{2}$AB,∠ADC的平分线交边BC于点E,AH⊥DE于点H,连接CH并延长交边AB于点F,连接AE交CF于点O.给出下列命题:①∠AEB=∠AEH;②DH=2$\sqrt{2}$EH;③HO=$\frac{1}{2}$AE;④BC-BF=$\sqrt{2}$EH
其中正确命题的序号是①③(填上所有正确命题的序号).
分析 根据矩形的性质得到AD=BC=$\sqrt{2}$AB=$\sqrt{2}$CD,由DE平分∠ADC,得到△ADH是等腰直角三角形,△DEC是等腰直角三角形,得到DE=$\sqrt{2}$CD,得到等腰三角形求出∠AED=67.5°,∠AEB=180°-45°-67.5°=67.5°,得到①正确;设DH=1,则AH=DH=1,AD=DE=$\sqrt{2}$,求出HE=$\sqrt{2}-1$,得到2$\sqrt{2}$HE=$2\sqrt{2}(\sqrt{2}-1)$≠1,故②错误;通过角的度数求出△AOH和△OEH是等腰三角形,从而得到③正确;由△AFH≌△CHE,到AF=EH,由△ABE≌△AHE,得到BE=EH,于是得到BC-BF=(BE+CE)-(AB-AF)=(CD+EH)-(CD-EH)=2EH,从而得到④错误.
解答 解:在矩形ABCD中,AD=BC=$\sqrt{2}$AB=$\sqrt{2}$CD,
∵DE平分∠ADC,
∴∠ADE=∠CDE=45°,
∵AH⊥DE,
∴△ADH是等腰直角三角形,
∴AD=$\sqrt{2}$AB,
∴AH=AB=CD,
∵△DEC是等腰直角三角形,
∴DE=$\sqrt{2}$CD,
∴AD=DE,
∴∠AED=67.5°,
∴∠AEB=180°-45°-67.5°=67.5°,
∴∠AED=∠AEB,
故①正确;
设DH=1,
则AH=DH=1,AD=DE=$\sqrt{2}$,
∴HE=$\sqrt{2}-1$,
∴2$\sqrt{2}$HE=$2\sqrt{2}(\sqrt{2}-1)$≠1,
故②错误;
∵∠AEH=67.5°,
∴∠EAH=22.5°,
∵DH=CD,∠EDC=45°,
∴∠DHC=67.5°,
∴∠OHA=22.5°,
∴∠OAH=∠OHA,
∴OA=OH,
∴∠AEH=∠OHE=67.5°,
∴OH=OE,
∴OH=$\frac{1}{2}$AE,
故③正确;
∵AH=DH,CD=CE,
在△AFH与△EHC中,
$\left\{\begin{array}{l}{∠AHF=∠HCE=22.5°}\\{∠FAH=∠HEC=45°}\\{AH=CE}\end{array}\right.$,
∴△AFH≌△EHC,
∴AF=EH,
在△ABE与△AHE中,
$\left\{\begin{array}{l}{AB=AH}\\{∠BEA=∠HEA}\\{AE=AE}\end{array}\right.$,
∴△ABE≌△AHE,
∴BE=EH,
∴BC-BF=(BE+CE)-(AB-AF)=(CD+EH)-(CD-EH)=2EH,
故④错误,
故答案为:①③.
点评 本题考查了矩形的性质,全等三角形的判定与性质,角平分线的定义,等腰三角形的判定与性质,熟记各性质并仔细分析题目条件,根据相等的度数求出相等的角,从而得到三角形全等的条件或判断出等腰三角形是解题的关键,也是本题的难点.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案| A. | 4cm | B. | 5cm | C. | 6cm | D. | 13cm |
| A. | 5.7×109 | B. | 5.7×1010 | C. | 0.57×1011 | D. | 57×109 |
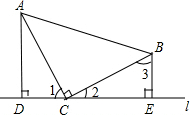 如图,在△ABC中,∠ACB=90°,CA=BC,直线l在△ABC的外部且过点C,AD⊥l,BE⊥l,垂足分别为点D、E.
如图,在△ABC中,∠ACB=90°,CA=BC,直线l在△ABC的外部且过点C,AD⊥l,BE⊥l,垂足分别为点D、E.
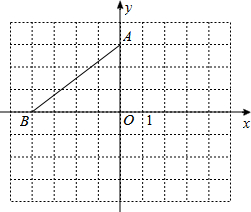 在平面直角坐标系中,点A的坐标是(0,3),点B在x轴上,将△AOB绕点A逆时针旋转90°得到△AEF,点O、B的对应点分别是点E、F.
在平面直角坐标系中,点A的坐标是(0,3),点B在x轴上,将△AOB绕点A逆时针旋转90°得到△AEF,点O、B的对应点分别是点E、F.
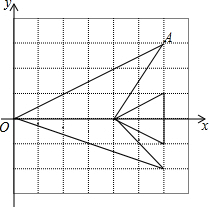 如图,将平面直角坐标系中“鱼”的每个“顶点”的纵坐标保持不变,横坐标分别变为原来的$\frac{1}{3}$,那么点A的对应点A′的坐标是(2,3).
如图,将平面直角坐标系中“鱼”的每个“顶点”的纵坐标保持不变,横坐标分别变为原来的$\frac{1}{3}$,那么点A的对应点A′的坐标是(2,3).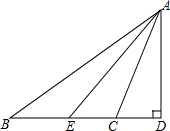 如图,△ABC中,AD是高,AE是角平分线,若∠ACB=110°,∠ABC=30°,求∠CAD和∠DAE的度数.
如图,△ABC中,AD是高,AE是角平分线,若∠ACB=110°,∠ABC=30°,求∠CAD和∠DAE的度数.