题目内容
如图,C是⊙O上的一点,过点C的⊙O的切线交直径AB的延长线于点P,若OB=PB=2
 ,则BC的长为 .
,则BC的长为 .


2
 .
.
【考点】切线的性质.
【分析】由切线的性质可知∠PCO=90°,再根据斜边中线定理即可解决问题.
【解答】解:如图,连接OC.
∵PC切⊙O于C,
∴OC⊥PC,
∴∠PCO=90°,
∵OB=PB,OB=2
 ,
,
∴BC=BO=PB=2
 ,
,
故答案为2
 .
.


【点评】本题考查切线的性质、直角三角形斜边中线定理,解题的关键是掌握切线的性质,知道切线垂直于过切点的半径,直角三角形斜边中线等于斜边一半,属于基础题.

练习册系列答案
相关题目

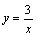 ,下列结论中,正确的是( )
,下列结论中,正确的是( )
 B.
B.
 C.
C.
 D.
D.


 D.﹣
D.﹣

 的开口向下,那么k的取值范围是__________.
的开口向下,那么k的取值范围是__________.