题目内容
1．已知ab=7，a+b=2，则多项式a2b+ab2+2001的值为2015．分析 原式前两项提取ab变形后，将已知等式代入计算即可求出值．
解答 解：原式=ab（a+b）+2001，
当ab=7，a+b=2时，原式=14+2001=2015，
故答案为：2015
点评 此题考查了因式分解-提公因式法，熟练掌握提取公因式的方法是解本题的关键．
练习册系列答案
小学生10分钟口算测试100分系列答案
相关题目
11．
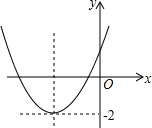已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，且关于x的一元二次方程ax2+bx+c-m=0没有实数根，有下列结论：
①abc＜0；②m＜-2；③b2-4ac＜0；④b2-4ac-8a=0
其中正确结论的序号是（ ）
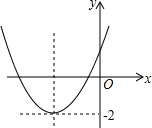已知二次函数y=ax2+bx+c（a≠0）的图象如图所示，且关于x的一元二次方程ax2+bx+c-m=0没有实数根，有下列结论：①abc＜0；②m＜-2；③b2-4ac＜0；④b2-4ac-8a=0
其中正确结论的序号是（ ）
| A． | ①④ | B． | ②③ | C． | ①② | D． | ②④ |
12．计算2x3•（-x2）的结果是（ ）
| A． | -2x5 | B． | 2x5 | C． | -2x6 | D． | 2x6 |
16．已知一三角形的三条中位线长分别为6、8、10，则这个三角形的周长是（ ）
| A． | 46 | B． | 48 | C． | 52 | D． | 130 |
6．某校初三一班组织了一次经典诵读比赛，甲、乙两队各10人的比赛成绩如下表（10分制）：
（1）写出甲队成绩的中位数和乙队成绩的众数；
（2）计算乙队的平均成绩和方差；
（3）已知甲队成绩的方差是1.4分2，则成绩较为整齐的是哪个队？
| 甲队 | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
| 乙队 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
（2）计算乙队的平均成绩和方差；
（3）已知甲队成绩的方差是1.4分2，则成绩较为整齐的是哪个队？
13．若a＞b，且c＜0，则下列不等式中正确的是（ ）
| A． | a÷c＜b÷c | B． | a×c＞b×c | C． | a+c＜b+c | D． | a-c＜b-c |
10．为促进学校之间的友谊，某县教育局组织了中学生友谊篮球赛，要求每两队之间都进行两次比赛，共要比赛90场，问共有多少个学校组队参加比赛？若设共有x个学校组队参加比赛，可列方程为（ ）
| A． | $\frac{1}{2}x（x-1）=90$ | B． | $\frac{1}{2}x（x+1）=90$ | C． | x（x-1）=90 | D． | x（x+1）=90 |
春耕期间，某农资门市部连续5填调进一批化肥销售．在开始调进化肥的第4天开始销售．若进货期间每天调入化肥的吨数与销售期间每天销售化肥的吨数都保持不变，这个门市部的化肥存量S（单位：t）与时间t（单位：天）之间的函数关系如图所示，则该门市部这次化肥销售活动（从开始进货到销售完毕）所用时间是7天．