题目内容
13.如图(仅供参考),已知在Rt△ABC中,∠ABC=90°,∠C=30°,AC=12cm,点E从点A出发沿AB以每秒1cm的速度向点B运动,同时点D从点C出发沿CA以每秒2cm的速度向点A运动,运动时间为t秒(0<t<6),过点D作DF⊥BC于点F.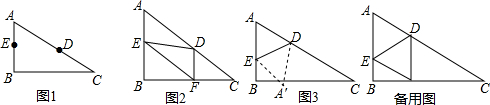
(1)用含t的式子表示 AE=t,AD=12-2t;
(2)如图2,在D、E运动的过程中,四边形AEFD是平行四边形,请说明理由;
(3)连接DE,当t=3或$\frac{24}{5}$时,△DEF为直角三角形;
(4)如图3,将△ADE沿DE翻折得到△A′DE,试问当t=4时,四边形AEA′D为菱形.请说明理由;
(5)在(4)的条件下,判断此时点A′是否在BC上.
分析 (1)根据题意直接表示出来即可;
(2)由“在直角三角形中,30度角所对的直角边是斜边的一半”求得DF=t,又AE=t,则DF=AE;而由垂直得到AB∥DF,即“四边形AEFD的对边平行且相等”,由此得四边形AEFD是平行四边形;
(3)①显然∠DFE<90°;
②如图1,当∠EDF=90°时,四边形EBFD为矩形,此时 AE=$\frac{1}{2}$AD,根据题意,列出关于t的方程,通过解方程来求t的值;
③如图2,当∠DEF=90°时,此时∠ADE=90°-∠A=30°,此时AD=$\frac{1}{2}$AE,根据题意,列出关于t的方程,通过解方程来求t的值;
(4)如图3,若四边形AEA′D为菱形,则AE=AD,则t=12-2t,所以t=4.即当t=4时,四边形AEA′D为菱形;
(5)根据直角三角形的性质得出GE=2BE,进而得出,GE=4=EA′,故点G与点A′重合,即可得出答案.
解答  (1)解:∵E从点A出发沿AB以每秒1cm的速度向点B运动,
(1)解:∵E从点A出发沿AB以每秒1cm的速度向点B运动,
∴AE=t,
∵点D从点C出发沿CA以每秒2cm的速度向点A运动,AC=12cm,
∴AD=12-2t;
故答案为:t,12-2t;
(2)证明:如图1,∵DF⊥BC,∠C=30°
∴DF=$\frac{1}{2}$CD=$\frac{1}{2}$×2t=t
∵AE=t
∴DF=AE,
∵∠ABC=90°,DF⊥BC
∴DF∥AE,
∴四边形AEFD是平行四边形;
(3)解:①显然∠DFE<90°;
②如图1,当∠EDF=90°时,四边形EBFD为矩形,
此时 AE=$\frac{1}{2}$AD=$\frac{1}{2}$×2t=t,
∴t=$\frac{1}{2}$(12-2t),
解得:t=3,
③如图2,当∠DEF=90°时,此时∠ADE=90°
∴∠AED=90°-∠A=30°
∴AD=$\frac{1}{2}$AE,
∴12-2t=$\frac{1}{2}$t
解得:t=$\frac{24}{5}$,
综上:当t=3秒或t=$\frac{24}{5}$秒时,△DEF为直角三角形;
故答案为:3或$\frac{24}{5}$;
(4)解:如图3,若四边形AEA′D为菱形,则AE=AD
则t=12-2t
解得:t=4
∴当t=4时,四边形AEA′D为菱形;
故答案为:4;
(5)解:设EA′交BC于点G
在Rt△EBG中,∠BEG=180°-∠AEG=60°,
则GE=2BE,
∵BE=AB-AE=6-4=2,
∴GE=4=EA′,
∴点G与点A′重合,
∴点A在BC上.
点评 本题考查了四边形综合题以及菱形的判定与性质和直角三角形的性质、平行四边形的判定等知识,解题时,需要分类讨论进而求出符合题意的答案.

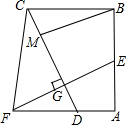 已知直角梯形ABCF中,AF∥BC,∠ABC=90°,点E为AB的中点,CD垂直平分EF于G,交AF于D,M为CG上一点,MG=EG,连BM下列结论:①若AE=AF,则CD=EF;②若EF=$\sqrt{2}$BM,则AB=AF;③若AE=2$\sqrt{2}$AD,则BC=5AD.其中正确的是( )
已知直角梯形ABCF中,AF∥BC,∠ABC=90°,点E为AB的中点,CD垂直平分EF于G,交AF于D,M为CG上一点,MG=EG,连BM下列结论:①若AE=AF,则CD=EF;②若EF=$\sqrt{2}$BM,则AB=AF;③若AE=2$\sqrt{2}$AD,则BC=5AD.其中正确的是( )| A. | 只有①② | B. | 只有②③ | C. | 只有①③ | D. | ①②③ |
| +3 | -4 | 0 | -2 | +4 | -1 |
(2)他们共做了多少个引体向上?
| A. | a>0,b>0 | B. | a<0,b<0 | C. | a、b同号 | D. | a、b异号 |
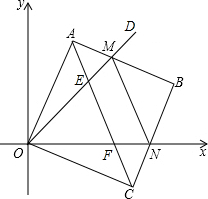 在平面直角坐标系中,边长为2的正方形OABC的两顶点A、C分别在y轴、x轴的正半轴上,点O在原点.现将正方形OABC绕O点顺时针旋转,当A点第一次落在第一象限的角平分线OD上时停止旋转,旋转过程中,AB边交OD于点M,BC边交x轴于点N,AC与OD相交于点E,与x轴相交于点F.(如图).
在平面直角坐标系中,边长为2的正方形OABC的两顶点A、C分别在y轴、x轴的正半轴上,点O在原点.现将正方形OABC绕O点顺时针旋转,当A点第一次落在第一象限的角平分线OD上时停止旋转,旋转过程中,AB边交OD于点M,BC边交x轴于点N,AC与OD相交于点E,与x轴相交于点F.(如图).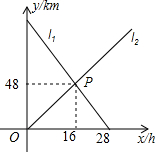 如图,小明从A地出发向B地行走,同时小亮从B地出发向A地行走,线段l1,l2分别表示小明、小亮离B地的距离与已用时间之间的关系,当x=0.5或2.7h时,小明与小亮相距7.7km.
如图,小明从A地出发向B地行走,同时小亮从B地出发向A地行走,线段l1,l2分别表示小明、小亮离B地的距离与已用时间之间的关系,当x=0.5或2.7h时,小明与小亮相距7.7km.