题目内容
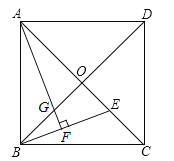
如图,正方形ABCD的对角线AC,BD相交于点O,AB=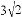 ,E为OC上一点,OE=1,连接BE,过点A作AF⊥BE于点F,与BD交于点G,则BF的长是( )
,E为OC上一点,OE=1,连接BE,过点A作AF⊥BE于点F,与BD交于点G,则BF的长是( )
A. 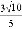 B.
B. 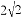 C.
C. 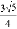 D.
D. 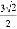
练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
题目内容
如图,正方形ABCD的对角线AC,BD相交于点O,AB=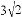 ,E为OC上一点,OE=1,连接BE,过点A作AF⊥BE于点F,与BD交于点G,则BF的长是( )
,E为OC上一点,OE=1,连接BE,过点A作AF⊥BE于点F,与BD交于点G,则BF的长是( )

A. 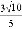 B.
B. 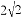 C.
C. 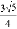 D.
D. 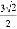
 字词句段篇系列答案
字词句段篇系列答案