ЬтФПФкШн
ЁОЬтФПЁПЪ§бЇПЮЩЯЃЌеХРЯЪІГіЪОСЫШчЯТПђжаЕФЬтФПЃЎ
вбжЊЃЌдк![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЕу
ЃЌЕу![]() ЮЊ
ЮЊ![]() ЕФжаЕуЃЌЕу
ЕФжаЕуЃЌЕу![]() КЭЕу
КЭЕу![]() ЗжБ№ЪЧБп
ЗжБ№ЪЧБп![]() КЭ
КЭ![]() ЩЯЕФЕуЃЌЧвЪМжеТњзу
ЩЯЕФЕуЃЌЧвЪМжеТњзу![]() ЃЌЪдШЗЖЈ
ЃЌЪдШЗЖЈ![]() гы
гы![]() ЕФДѓаЁЙиЯЕЃЎ
ЕФДѓаЁЙиЯЕЃЎ

аЁУїгыЭЌзРаЁДЯЬжТлКѓЃЌНјааСЫШчЯТНтД№ЃК

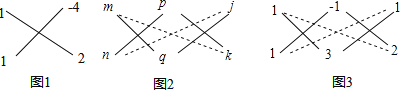
ЃЈ1ЃЉЃЈЬиЪтЧщПіЃЌЬНЫїНсТлЃЉШчЭМ1ЃЌШєЕу![]() гыЕу
гыЕу![]() жиКЯЪБЃЌЕу
жиКЯЪБЃЌЕу![]() гыЕу
гыЕу![]() жиКЯЃЌШнвзЕУЕН
жиКЯЃЌШнвзЕУЕН![]() гы
гы![]() ЕФДѓаЁЙиЯЕЃЎЧыФужБНгаДГіНсТлЃК
ЕФДѓаЁЙиЯЕЃЎЧыФужБНгаДГіНсТлЃК![]() ____________
____________![]() ЃЈЬюЁА
ЃЈЬюЁА![]() ЁБЃЌЁА
ЁБЃЌЁА![]() ЁБЛђЁА
ЁБЛђЁА![]() ЁБЃЉЃЎ
ЁБЃЉЃЎ
ЃЈ2ЃЉЃЈЬиР§ЦєЗЂЃЌНтД№ЬтФПЃЉШчЭМ2ЃЌШєЕу![]() ВЛгыЕу
ВЛгыЕу![]() жиКЯЪБЃЌ
жиКЯЪБЃЌ![]() гы
гы![]() ЕФДѓаЁЙиЯЕЪЧЃК
ЕФДѓаЁЙиЯЕЪЧЃК![]() _________
_________![]() ЃЈЬюЁА
ЃЈЬюЁА![]() ЁБЃЌЁА
ЁБЃЌЁА![]() ЁБЛђЁА
ЁБЛђЁА![]() ЁБЃЉЃЎРэгЩШчЯТЃКСЌНс
ЁБЃЉЃЎРэгЩШчЯТЃКСЌНс![]() ЃЌЃЈЧыФуЭъГЩЪЃЯТЕФНтД№Й§ГЬЃЉ
ЃЌЃЈЧыФуЭъГЩЪЃЯТЕФНтД№Й§ГЬЃЉ
ЃЈ3ЃЉЃЈЭиеЙНсТлЃЌЩшМЦаТЬтЃЉдк![]() жа
жа![]() ЃЌ
ЃЌ![]() ЃЌЕу
ЃЌЕу![]() ЮЊ
ЮЊ![]() ЕФжаЕуЃЌЕу
ЕФжаЕуЃЌЕу![]() КЭЕу
КЭЕу![]() ЗжБ№ЪЧжБЯп
ЗжБ№ЪЧжБЯп![]() КЭжБЯп
КЭжБЯп![]() ЩЯЕФЕуЃЌЧвЪМжеТњзу
ЩЯЕФЕуЃЌЧвЪМжеТњзу![]() ЃЌШє
ЃЌШє![]() ЃЌ
ЃЌ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФГЄЃЎЃЈЧыФужБНгаДГіНсЙћЃЉ
ЕФГЄЃЎЃЈЧыФужБНгаДГіНсЙћЃЉ
ЁОД№АИЁПЃЈ1ЃЉ=ЃЛЃЈ2ЃЉ=ЃЌРэгЩМћНтЮіЃЛЃЈ3ЃЉ1Лђ3
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЕШжБНЧШ§НЧаЮаББпЕФжаЯпЕШгкаББпЕФвЛАыНтД№МДПЩЃЛ
ЃЈ2ЃЉСЌНс![]() ЃЌжЄУїЁїBDEЁеЁїADFМДПЩЃЛ
ЃЌжЄУїЁїBDEЁеЁїADFМДПЩЃЛ
ЃЈ3ЃЉЗжЫФжжЧщПіЧѓНтЃКЂйЕБЕуEдкBAЕФбгГЄЯпЩЯЃЌЕуFдкACЕФбгГЄЯпЩЯЃЛЂкЕБЕуEдкABЕФбгГЄЯпЩЯЃЌЕуFдкCAЕФбгГЄЯпЩЯЃЛЂлЕБЕуEдкABЕФбгГЄЯпЩЯЃЌЕуFдкACЕФбгГЄЯпЩЯЃЛЂмЕБЕуEдкBAЕФбгГЄЯпЩЯЃЌЕуFдкCAЕФбгГЄЯпЩЯЃЎ
ЃЈ1ЃЉЁп![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
ЁрЁЯACD=45Ёу.
Ёп![]() ЃЌЕу
ЃЌЕу![]() ЮЊ
ЮЊ![]() ЕФжаЕуЃЌ
ЕФжаЕуЃЌ
ЁрЁЯCAD=45ЁуЃЌ
ЁрЁЯCAD=ЁЯACDЃЌ
ЁрAD=CDЃЌ
МДDE=DFЃЛ
ЃЈ2ЃЉСЌНс![]() ЃЌ
ЃЌ
Ёп![]() ЃЌЕу
ЃЌЕу![]() ЮЊ
ЮЊ![]() ЕФжаЕуЃЌ
ЕФжаЕуЃЌ
ЁрAD=![]() =BDЃЎ
=BDЃЎ
Ёп![]() ЃЌ
ЃЌ![]() ЃЌЕу
ЃЌЕу![]() ЮЊ
ЮЊ![]() ЕФжаЕуЃЌ
ЕФжаЕуЃЌ
ЁрЁЯB=ЁЯC=ЁЯCAD=ЁЯBAD=45ЁуЃЌADЁЭBCЃЌ
ЁрЁЯADE+ЁЯBDE=90ЁуЃЎ
ЁпDEЁЭDFЃЌ
ЁрЁЯADE+ЁЯADF=90ЁуЃЌ
ЁрЁЯBDE=ЁЯADFЃЎ
дкЁїBDEКЭЁїADFжаЃЌ
ЁпЁЯB=ЁЯCAD=45ЁуЃЌ
AD=BDЃЌ
ЁЯBDE=ЁЯADFЃЌ
ЁрЁїBDEЁеЁїADFЃЌ
ЁрDE=DFЃЛ
ЃЈ3ЃЉЂйЕБЕуEдкBAЕФбгГЄЯпЩЯЃЌЕуFдкACЕФбгГЄЯпЩЯЃЌШчЭМ1ЃЌ
гЩЃЈ2ЃЉжЊЃЌAD=CDЃЌЁЯCAD=ЁЯACB=45ЁуЃЌ
ЁрЁЯDAE=ЁЯDCE=135ЁуЃЎ
ЁпDEЁЭDFЃЌEЁЭDFЃЌ
ЁрЁЯCDE+ЁЯCDF=90ЁуЃЌЁЯADE+ЁЯCDE=90ЁуЃЌ
ЁрЁЯCDF=ЁЯADEЃЌ
дкЁїADEКЭЁїCDFжаЃЌ
ЁпЁЯDAE=ЁЯDCEЃЌ
AD=CDЃЌ
ЁЯADE=ЁЯCDFЃЌ
ЁрЁїADEЁеЁїCDFЃЌ
ЁрCF=AEЃЌ
ЁпBE=2ЃЌЃЌAB=1ЃЌ
ЁрCF=AE=2-1=1ЃЛ
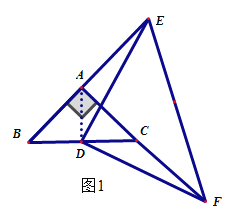
ЂкЕБЕуEдкABЕФбгГЄЯпЩЯЃЌЕуFдкCAЕФбгГЄЯпЩЯЃЌШчЭМ2ЃЌ
гыЂйЭЌРэПЩжЄЁїADFЁеЁїBDEЃЌ
ЁрAF=BE=2ЃЌ
ЁпAC=1ЃЌ
ЁрCF=2+1=3ЃЛ
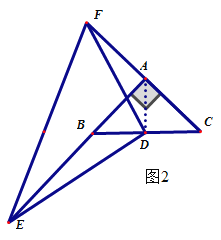
ЂлЕБЕуEдкABЕФбгГЄЯпЩЯЃЌЕуFдкACЕФбгГЄЯпЩЯЃЌШчЭМ3ЃЌ СЌНгADЃЌВЂбгГЄНЛEFгыHЃЌ
ЁпЁЯ5=ЁЯ1+ЁЯ3ЃЌЁЯ6=ЁЯ2+ЁЯ4ЃЌ
ЁрЁЯ5+ЁЯ6=ЁЯ1+ЁЯ3+ЁЯ2+ЁЯ4ЃЌ
ЁпЁЯ1+ЁЯ2=90ЁуЃЌЁЯ5+ЁЯ6=90ЁуЃЌ
ЁрЁЯ3+ЁЯ4=0ЁуЃЌВЛКЯЬтвтЃЌДЫжжЧщПіВЛГЩСЂЃЛ

ЂмЕБЕуEдкBAЕФбгГЄЯпЩЯЃЌЕуFдкCAЕФбгГЄЯпЩЯЃЌШчЭМ4ЃЌ
ЭЌЂлЕФЗНЗЈПЩЫЕУїДЫжжЧщПівВВЛГЩСЂЃЎ
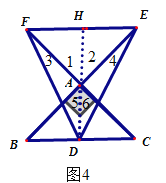
злЩЯПЩжЊЃЌCFЕФГЄЪЧ1Лђ3ЃЎ