题目内容
7. 在等边△ABC中,点D,E分别在边BC、AC上,若CD=2,过点D作DE∥AB,过点E作EF⊥DE,交BC的延长线于点F,求EF的长.
在等边△ABC中,点D,E分别在边BC、AC上,若CD=2,过点D作DE∥AB,过点E作EF⊥DE,交BC的延长线于点F,求EF的长.
分析 先证明△DEC是等边三角形,再在RT△DEC中求出EF即可解决问题.
解答 解: ∵△ABC是等边三角形,
∵△ABC是等边三角形,
∴∠B=∠ACB=60°,
∵DE∥AB,
∴∠EDC=∠B=60°,
∴△EDC是等边三角形,
∴DE=DC=2,
在RT△DEF中,∵∠DEF=90°,DE=2,
∴DF=2DE=4,
∴EF=$\sqrt{D{F}^{2}-D{E}^{2}}$=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$.
点评 不同考查等边三角形的性质、直角三角形中30度角所对的直角边等于斜边的一半,勾股定理等知识,解题的关键是利用特殊三角形解决问题,属于中考常考题型.

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案
相关题目
15.下列事件为必然事件的是( )
| A. | 王华期末考试数学成绩会是100分 | |
| B. | 某射击运动员射靶一次,正中靶心 | |
| C. | 打开电视机,CCTV第一套节目正在播放新闻 | |
| D. | 口袋中装有2个红球和一个白球,从中摸出2个球,其中必有红球 |
12.在不透明口袋内有形状、大小、质地完全一样的5个小球,其中红球3个,白球2个,随机抽取一个小球是红球的概率是( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{5}$ | D. | $\frac{2}{5}$ |
19.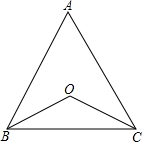 如图,点O在△ABC内,且到三边的距离相等.若∠BOC=120°,则tanA的值为( )
如图,点O在△ABC内,且到三边的距离相等.若∠BOC=120°,则tanA的值为( )
 如图,点O在△ABC内,且到三边的距离相等.若∠BOC=120°,则tanA的值为( )
如图,点O在△ABC内,且到三边的距离相等.若∠BOC=120°,则tanA的值为( )| A. | $\sqrt{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{2}}{2}$ |
16.某校随机抽查了10名参加2016年云南省初中学业水平考试学生的体育成绩,得到的结果如表:
下列说法正确的是( )
| 成绩(分) | 46 | 47 | 48 | 49 | 50 |
| 人数(人) | 1 | 2 | 1 | 2 | 4 |
| A. | 这10名同学的体育成绩的众数为50 | |
| B. | 这10名同学的体育成绩的中位数为48 | |
| C. | 这10名同学的体育成绩的方差为50 | |
| D. | 这10名同学的体育成绩的平均数为48 |
 如图,矩形ABCD在第一象限,四边分别平行于x轴和y轴,且顶点A、C在反比例函数图象上,BA延长线交y轴于点E,BC延长线交x轴于点F,S△AOE=$\frac{1}{2}$.
如图,矩形ABCD在第一象限,四边分别平行于x轴和y轴,且顶点A、C在反比例函数图象上,BA延长线交y轴于点E,BC延长线交x轴于点F,S△AOE=$\frac{1}{2}$.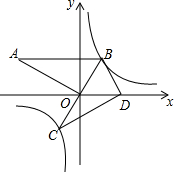 在平面直角坐标系中双曲线$y=\frac{k}{x}$经过△CDB顶点B,边BC过坐标原点O,点D在x轴的正半轴上,且∠BDC=90°,现将△CDB绕点B顺时针旋转得到对应△AOB如图所示,此时AB∥x轴,OA=$2\sqrt{3}$.则k的值是( )
在平面直角坐标系中双曲线$y=\frac{k}{x}$经过△CDB顶点B,边BC过坐标原点O,点D在x轴的正半轴上,且∠BDC=90°,现将△CDB绕点B顺时针旋转得到对应△AOB如图所示,此时AB∥x轴,OA=$2\sqrt{3}$.则k的值是( )