题目内容
 阅读理解题:
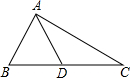
阅读理解题:如图,在△ABC中,AD是BC边上的中线,且AD=
| 1 |
| 2 |
求证:∠BAC=90°.
证明:∵AD=
| 1 |
| 2 |
| 1 |
| 2 |
∴AD=BD=DC,
∴△ADB和△ADC都是等腰三角形
∴∠B=∠BAD,∠C=∠CAD,
∵∠B+∠BAD+∠CAD+∠C=180°,
∴∠BAD+∠CAD=90°,即∠BAC=90°.
(1)此题实际上是直角三角形的一个判定方法,请你用文字语言叙述出来.
(2)直接运用这个结论解答题目:一个三角形一边长为2,这边上的中线长为1,另两边之和为1+
| 3 |
【知识储备:勾股定理:在直角三角形中.两直角边的平方和等于斜边的平方】.
考点:勾股定理,直角三角形斜边上的中线
专题:阅读型
分析:(1)根据直角三角形的判定定理即可得出结论;
(2)设这个直角三角形的两条直角边的长分别为a、b,根据勾股定理可求出ab与a+b的值,再根据直角三角形的面积公式即可得出结论.
(2)设这个直角三角形的两条直角边的长分别为a、b,根据勾股定理可求出ab与a+b的值,再根据直角三角形的面积公式即可得出结论.
解答:解:(1)如果一个三角形的一边上的中线的长等于这条边长的一半,那么这个三角形是直角三角形;
(2)因为这个三角形的一条边上的中线长是这条边长的一半,所以这个三角形是直角三角形.
设这个直角三角形的两条直角边的长分别为a、b,则a+b=1+
根据勾股定理,得a2+b2=22,即a2+b2=4,
∵(a+b)2=a2+b2+2ab,即(1+
)2=4+2ab,
∴ab=
,
∴S=
ab=
,
∴这个三角形的面积为
.
(2)因为这个三角形的一条边上的中线长是这条边长的一半,所以这个三角形是直角三角形.
设这个直角三角形的两条直角边的长分别为a、b,则a+b=1+
| 3 |
根据勾股定理,得a2+b2=22,即a2+b2=4,
∵(a+b)2=a2+b2+2ab,即(1+
| 3 |
∴ab=
| 3 |
∴S=
| 1 |
| 2 |
| ||
| 2 |
∴这个三角形的面积为
| ||
| 2 |
点评:本题考查的是勾股定理,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.

练习册系列答案
相关题目
一个两位数,个位是a,十位是b,这个两位数是( )
| A、ab | B、10a+b |
| C、10b+a | D、a+b |
已知
+(b-1)2=0,则(a+b)2014的值是( )
| a+2 |
| A、-1 | B、1 |
| C、2014 | D、-2014 |
有理数0.0050400的有效数字的个数是( )
| A、3个 | B、4个 | C、5个 | D、6个 |
 如图,已知y=-x+1与x轴、y轴分别交于A、B两点,P为双曲线y=
如图,已知y=-x+1与x轴、y轴分别交于A、B两点,P为双曲线y=