题目内容
 如图,已知y=-x+1与x轴、y轴分别交于A、B两点,P为双曲线y=
如图,已知y=-x+1与x轴、y轴分别交于A、B两点,P为双曲线y=| 1 |
| 2x |
考点:反比例函数综合题
专题:证明题
分析:首先设P(a,b),由E和F都在直线y=-x+1上,可求得BE=
a,AF=
b,又由直线y=-x+1分别交x轴、y轴于A,B两点,可得△AOB为等腰直角三角形,易证得△AOF∽△BEO,即可得∠FOE=∠OBE=45°.
| 2 |
| 2 |
解答:证明:设P(a,b),
则OM=a,PM=b,
∴点E的横坐标为a,F的纵坐标为b,
又∵E和F都在直线y=-x+1上,
∴点E(a,1-a),点F(1-b,b),
即OM=a,EM=1-a,ON=b,NF=1-b,
∵BE=
=
a,AF=
=
b,
∵直线y=-x+1分别交x轴、y轴于A,B两点,
∴令x=0,求出y=1,即B(0,1);令y=0,求出x=1,即A(1,0),
∵OA=OB=1,且∠AOB=90°,
即△AOB为等腰直角三角形,
∴∠FAO=∠EBO=45°,
∵点P(a,b)是曲线y=
上一点,
∴2ab=1,
即AF•BE=
a•
b=2ab=1,
又∵OA•OB=1,
∴
=
,
∴△AOF∽△BEO,
∴∠AFO=∠BOE,
又∵∠BOE=∠BOF+∠FOE,∠AFO=∠OBF+∠BOF,
∴∠FOE=∠OBE=45°.
则OM=a,PM=b,
∴点E的横坐标为a,F的纵坐标为b,
又∵E和F都在直线y=-x+1上,
∴点E(a,1-a),点F(1-b,b),
即OM=a,EM=1-a,ON=b,NF=1-b,
∵BE=
| a2+(1-1+a)2 |
| 2 |
| (1-1+b)2+b2 |
| 2 |
∵直线y=-x+1分别交x轴、y轴于A,B两点,
∴令x=0,求出y=1,即B(0,1);令y=0,求出x=1,即A(1,0),
∵OA=OB=1,且∠AOB=90°,
即△AOB为等腰直角三角形,
∴∠FAO=∠EBO=45°,
∵点P(a,b)是曲线y=
| 1 |
| 2x |
∴2ab=1,
即AF•BE=
| 2 |
| 2 |
又∵OA•OB=1,
∴
| AF |
| OB |
| OA |
| BE |
∴△AOF∽△BEO,
∴∠AFO=∠BOE,
又∵∠BOE=∠BOF+∠FOE,∠AFO=∠OBF+∠BOF,
∴∠FOE=∠OBE=45°.
点评:此题属于反比例函数综合题,考查了等腰直角三角形的性质、相似三角形的判定与性质以及点与函数的关系.此题难度较大,注意掌握数形结合思想与方程思想的应用.

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
在给出的四个方程中,解相同的为( )
①x-2=3;②(x-2)(x-5)=0;③2x-3=7;④x=5.
①x-2=3;②(x-2)(x-5)=0;③2x-3=7;④x=5.
| A、①② | B、①③④ | C、②③ | D、②④ |
 如图,下列条件中,不能证明△ABD≌△ACD的是( )
如图,下列条件中,不能证明△ABD≌△ACD的是( )| A、AB=AC,BD=CD |
| B、∠B=∠C,∠BAD=∠CAD |
| C、∠B=∠C,BD=CD |
| D、∠ADB=∠ADC,DB=DC |
在5,2006,0,-2
,-
中,负数有( )
| 1 |
| 2 |
| 1 |
| 3 |
| A、0个 | B、1个 | C、2个 | D、3个 |
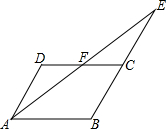 如图,四边形ABCD是平行四边形.点E在BC的延长线上,且CE=BC,连接AE交DC于点F.
如图,四边形ABCD是平行四边形.点E在BC的延长线上,且CE=BC,连接AE交DC于点F. 如图,在Rt△ABC中,∠C=90°,AC=8
如图,在Rt△ABC中,∠C=90°,AC=8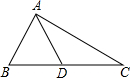 阅读理解题:
阅读理解题: