题目内容
三个边长为1的正方形并列放在一条直线l上,将中间的正方形抽出并旋转45°,如图所示,然后对准中心朝原来的位置放下,直到碰触到原来两边的正方形,此时从B点新位置到原来底边直线l的距离是________.
 +
+
分析:如图:点B到L的距离为对角线BE的长度加上边长再减去OE的长度.
解答:
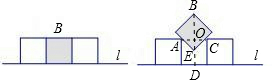
解:由于正方形是旋转45°由正方形的性质可得出:∠ECO=∠EAO=45°,EA=EC;
又由∠AEC=90°则EA2+EC2=AC2,AC=1.
所以AE=
 根据面积公式得:AE×CE=OE×AC
根据面积公式得:AE×CE=OE×AC所以OE=
 ;
;对角线BE=

所以B距L的距离BD=BE+OD-OE=
 +
+ .
.故答案为:
 +
+ .
.点评:此题重点在于作出图形,由题意得出∠ECO=∠EAO=45°,通过勾股定理和面积公式得出OE的长度.

练习册系列答案
相关题目
 如图,用三个边长为1的正方形组成一个轴对称图形,求能将三个正方形完全覆盖的圆的最小半径.
如图,用三个边长为1的正方形组成一个轴对称图形,求能将三个正方形完全覆盖的圆的最小半径.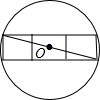 要将三个边长为1的正方形放在一个圆碟内,要求这三个正方形不能有某部分在碟边以外,且不能重叠,问圆碟的半径至少是多少?(如图就是一种放法,此时圆碟的直径至少是长方形对角线,即
要将三个边长为1的正方形放在一个圆碟内,要求这三个正方形不能有某部分在碟边以外,且不能重叠,问圆碟的半径至少是多少?(如图就是一种放法,此时圆碟的直径至少是长方形对角线,即
 三个边长为1的正方形的底边并列在一条直线上,将中间的正方形ABCD向上平移1个单位,再绕中心顺时针旋转45°,然后向下平移,直到碰触到原来两边的正方形,得到正方形A′B′C′D′,如图所示,则A′点到原来底边直线的距离是
三个边长为1的正方形的底边并列在一条直线上,将中间的正方形ABCD向上平移1个单位,再绕中心顺时针旋转45°,然后向下平移,直到碰触到原来两边的正方形,得到正方形A′B′C′D′,如图所示,则A′点到原来底边直线的距离是