Question

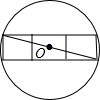要将三个边长为1的正方形放在一个圆碟内，要求这三个正方形不能有某部分在碟边以外，且不能重叠，问圆碟的半径至少是多少？（如图就是一种放法，此时圆碟的直径至少是长方形对角线，即

10

，故半径至少是

10

2

），请你设计一种，并通过计算指出你认为半径最小的设计方案（画出图）

Answer 1

分析：根据题意画出图形，根据勾股定理可分别求出三种情况中圆的半径，再进行比较即可．

解答：解：由图可知，（一）、（二）两种图形中所求的圆碟均以O点为圆心，以OA为半径，则OA=

2

；
当如图（三）所示时，此时圆碟的半径r=OE=OD＜

2

，设此时圆心为O，OF=x，则OC=2-x，
故在Rt△OEF与Rt△OCD中，

x2+ 1 4 =r2 (2-x)2+1=r2

，解得r=

5 17

16

，
因为

5 17

16

＜

2

＜

10

2

，所以圆碟的半径至少是

5 17

16

．

点评：本题比较复杂，解答此题的关键是根据题意画出可能出现的三种情况，分别求出圆碟的半径，再进行比较．