题目内容
 三个边长为1的正方形的底边并列在一条直线上,将中间的正方形ABCD向上平移1个单位,再绕中心顺时针旋转45°,然后向下平移,直到碰触到原来两边的正方形,得到正方形A′B′C′D′,如图所示,则A′点到原来底边直线的距离是
三个边长为1的正方形的底边并列在一条直线上,将中间的正方形ABCD向上平移1个单位,再绕中心顺时针旋转45°,然后向下平移,直到碰触到原来两边的正方形,得到正方形A′B′C′D′,如图所示,则A′点到原来底边直线的距离是| 2 |
| 1 |
| 2 |
| 2 |
| 1 |
| 2 |
分析:如图:点A′到l的距离为对角线A′C′的长度加上边长再减去C′E的长度.
解答: 解:如图,连接A′C′、FG交于点O,并延长A′C′交l于点E.
解:如图,连接A′C′、FG交于点O,并延长A′C′交l于点E.
∵正方形是A′B′C′D′是由正方形ABCD旋转45°后得到的,
∴由正方形的性质可得出:∠FC′O=∠GC′O=45°,FC′=GC′;
又∵∠FC′G=90°,
∴FC′2+GC′2=FG2,FG=1.
∴FC′=
,根据面积公式得:FC′×GC′=OC′×FG,
∴OC′=
;
对角线A′C′=
,
∴A′距l的距离A′E=A′C′+OE-OC′=
+
.
故答案是:
+
.
 解:如图,连接A′C′、FG交于点O,并延长A′C′交l于点E.
解:如图,连接A′C′、FG交于点O,并延长A′C′交l于点E.∵正方形是A′B′C′D′是由正方形ABCD旋转45°后得到的,
∴由正方形的性质可得出:∠FC′O=∠GC′O=45°,FC′=GC′;
又∵∠FC′G=90°,
∴FC′2+GC′2=FG2,FG=1.
∴FC′=
| ||
| 2 |
∴OC′=
| 1 |
| 2 |
对角线A′C′=
| 2 |
∴A′距l的距离A′E=A′C′+OE-OC′=
| 2 |
| 1 |
| 2 |
故答案是:
| 2 |
| 1 |
| 2 |
点评:本题考查了旋转的性质.此题重点在于作出图形,由题意得出:∠D′C′O=∠B′C′O=45°,通过勾股定理和面积公式得出OE的长度.

练习册系列答案
相关题目
 如图,用三个边长为1的正方形组成一个轴对称图形,求能将三个正方形完全覆盖的圆的最小半径.
如图,用三个边长为1的正方形组成一个轴对称图形,求能将三个正方形完全覆盖的圆的最小半径.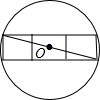 要将三个边长为1的正方形放在一个圆碟内,要求这三个正方形不能有某部分在碟边以外,且不能重叠,问圆碟的半径至少是多少?(如图就是一种放法,此时圆碟的直径至少是长方形对角线,即
要将三个边长为1的正方形放在一个圆碟内,要求这三个正方形不能有某部分在碟边以外,且不能重叠,问圆碟的半径至少是多少?(如图就是一种放法,此时圆碟的直径至少是长方形对角线,即