题目内容
AB是⊙O的弦,∠AOB=70°,则AB所对的圆周角是
- A.35°
- B.70°或110°
- C.55°
- D.35°或145°
D
分析:首先根据题意作图,由AB是⊙O的弦,∠AOB=70°,根据在同圆或等圆中,同弧或等弧所对的圆周角等于这条弧所对的圆心角的一半,即可求得∠ACB的度数,又圆的内接四边形的性质,求得∠AC′B的度数,继而可得答案.
解答: 解:如图:∵AB是⊙O的弦,∠AOB=70°,
解:如图:∵AB是⊙O的弦,∠AOB=70°,
∴∠ACB= ∠AOB=35°,
∠AOB=35°,
∵四边形ACBC′是⊙O的内接四边形,
∴∠AC′B+∠ACB=180°,
∴∠AC′B=145°,
∴AB所对的圆周角是:35°或145°.
故选D.
点评:此题考查了圆周角的性质与圆的内接四边形的性质.此题难度不大,解题的关键是注意数形结合思想的应用,注意弦AB所对的圆周角分为两种且互补.
分析:首先根据题意作图,由AB是⊙O的弦,∠AOB=70°,根据在同圆或等圆中,同弧或等弧所对的圆周角等于这条弧所对的圆心角的一半,即可求得∠ACB的度数,又圆的内接四边形的性质,求得∠AC′B的度数,继而可得答案.
解答:
 解:如图:∵AB是⊙O的弦,∠AOB=70°,
解:如图:∵AB是⊙O的弦,∠AOB=70°,∴∠ACB=
 ∠AOB=35°,
∠AOB=35°,∵四边形ACBC′是⊙O的内接四边形,
∴∠AC′B+∠ACB=180°,
∴∠AC′B=145°,
∴AB所对的圆周角是:35°或145°.
故选D.
点评:此题考查了圆周角的性质与圆的内接四边形的性质.此题难度不大,解题的关键是注意数形结合思想的应用,注意弦AB所对的圆周角分为两种且互补.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
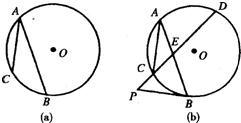 14、如图,已知AC、AB是⊙O的弦,AB>AC.
14、如图,已知AC、AB是⊙O的弦,AB>AC.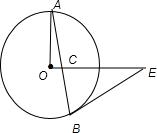
 如图,AB是⊙0的弦,BC与⊙0相切于点B,连接OA、OB.若∠ABC=70°,则∠A等于
如图,AB是⊙0的弦,BC与⊙0相切于点B,连接OA、OB.若∠ABC=70°,则∠A等于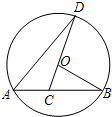 如图,已知AB是⊙O的弦,C是弦AB上的任意一点(不与点A、B重合),连接CO并延长,CO交⊙O于点D,连接AD.若∠B=30°,∠D=20°,则∠BOD的度数为
如图,已知AB是⊙O的弦,C是弦AB上的任意一点(不与点A、B重合),连接CO并延长,CO交⊙O于点D,连接AD.若∠B=30°,∠D=20°,则∠BOD的度数为