Question

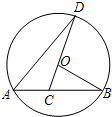如图，已知AB是⊙O的弦，C是弦AB上的任意一点（不与点A、B重合），连接CO并延长，CO交⊙O于点D，连接AD．若∠B=30°，∠D=20°，则∠BOD的度数为

100°

．

Answer 1

分析：由三角形外角的性质，可得：∠BOD=∠B+∠BCO，∠BCO=∠A+∠D．又由圆周角定理，可得：2∠A=∠B+∠A+∠D=∠A+50°，则可求得∠A的度数，继而求得答案．

解答：解：∵∠BOD=∠B+∠BCO，∠BCO=∠A+∠D．
∴∠BOD=∠B+∠A+∠D，
又∵∠BOD=2∠A，∠B=30°，∠D=20°，
∴2∠A=∠B+∠A+∠D=∠A+50°，
解得：∠A=50°，
∴∠BOD=2∠A=100°．
故答案为：100°．

点评：此题考查了圆周角定理以及三角形外角的性质．此题难度不大，注意掌握数形结合思想的应用．