题目内容
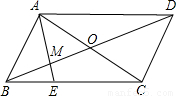
 如图?ABCD,O为对角线的交点,E为BC上一点,BE:EC=1:2,则BM:MO:OD=
如图?ABCD,O为对角线的交点,E为BC上一点,BE:EC=1:2,则BM:MO:OD=
- A.2:2:3
- B.2:3:4
- C.1:1:2
- D.2:3:5
C
分析:作OF∥AE,根据平行四边形的性质,可得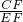 =
=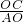 =
= ,可得CF=EF,又BE:EC=1:2,可得BE=EF=FC,所以,
,可得CF=EF,又BE:EC=1:2,可得BE=EF=FC,所以, =
= =
= ,又因为OB=OD,所以,即可得出所求;
,又因为OB=OD,所以,即可得出所求;
解答: 解:∵四边形ABCD是平行四边形,
解:∵四边形ABCD是平行四边形,
∴OC=AO,OB=OD,
如图,作OF∥AE,
∴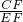 =
=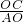 =
= ,
,
∴CF=EF,
又∵BE:EC=1:2,
∴BE=EF=FC,
∴ =
= =
= ,
,
又∵OB=OD,
∴BM:MO:OD=1:1:2.
故选C.
点评:本题主要考查了平行线分线段成比例和平行线的性质,作辅助线OF∥AE,构建平行线成比例,是解答本题的关键.
分析:作OF∥AE,根据平行四边形的性质,可得
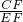 =
=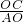 =
= ,可得CF=EF,又BE:EC=1:2,可得BE=EF=FC,所以,
,可得CF=EF,又BE:EC=1:2,可得BE=EF=FC,所以, =
= =
= ,又因为OB=OD,所以,即可得出所求;
,又因为OB=OD,所以,即可得出所求;解答:
 解:∵四边形ABCD是平行四边形,
解:∵四边形ABCD是平行四边形,∴OC=AO,OB=OD,
如图,作OF∥AE,
∴
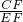 =
=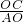 =
= ,
,∴CF=EF,
又∵BE:EC=1:2,
∴BE=EF=FC,
∴
 =
= =
= ,
,又∵OB=OD,
∴BM:MO:OD=1:1:2.
故选C.
点评:本题主要考查了平行线分线段成比例和平行线的性质,作辅助线OF∥AE,构建平行线成比例,是解答本题的关键.

练习册系列答案
相关题目
 如图?ABCD,O为对角线的交点,E为BC上一点,BE:EC=1:2,则BM:MO:OD=( )
如图?ABCD,O为对角线的交点,E为BC上一点,BE:EC=1:2,则BM:MO:OD=( )| A、2:2:3 | B、2:3:4 | C、1:1:2 | D、2:3:5 |
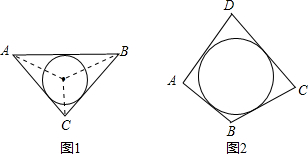 阅读材料:如图1,△ABC的周长为l,面积为S,内切圆O的半径为r,探究r与S、l之间的关系.连接OA,OB,OC∵S=S△OAB+S△OBC+S△OCA
阅读材料:如图1,△ABC的周长为l,面积为S,内切圆O的半径为r,探究r与S、l之间的关系.连接OA,OB,OC∵S=S△OAB+S△OBC+S△OCA 长度足够长),并利用已有总长为40米的铁围栏,设BC=x米,矩形车棚的面积为y平方米
长度足够长),并利用已有总长为40米的铁围栏,设BC=x米,矩形车棚的面积为y平方米