题目内容
 (1)对于正数x,规定f(x)=
(1)对于正数x,规定f(x)=| x |
| 1+x |
| 3 |
| 1+3 |
| 3 |
| 4 |
| 1 |
| 3 |
| ||
1+
|
| 1 |
| 4 |
计算:f(
| 1 |
| 2009 |
| 1 |
| 2008 |
| 1 |
| 2007 |
| 1 |
| 3 |
| 1 |
| 2 |
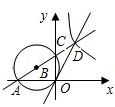
(2)已知:如图,O为平面直角坐标系的原点,半径为1的⊙B经过点O,且与x,y轴分交于点A,C,点A的坐标为(-
| 3 |
分析:(1)可以发现f(n)+f(
)=1,故原式可化为:
+1+1+1+…+1+1+1,共有2008个1,故可得到结果.
(2)由AC为直径,可知AC=2,有OA=
,则在Rt△ABC中,由勾股定理求得OC的值,再由正弦的概念求得∠CAO的度数.
| 1 |
| n |
| 1 |
| 2 |
(2)由AC为直径,可知AC=2,有OA=
| 3 |
解答:解:
(1)∵f(1)=
=
,f(2)=
=
,f(
)=
=
,f(3)=
,f(
)=
;
∴f(1)=
;f(2)+f(
)=1;f(3)+f(
)=1;f(n)+f(
)=1
原式=f(1)+f(2)+f(
)+f(3)+f(
)+f(2008)+f(
)+f(2009)+f(
)
=
+1+1+1+…+1+1+1
=2008
;
(2)
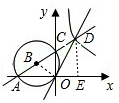
∵∠AOC=90°,
∴AC是⊙B的直径,
∴AC=2
又∵点A的坐标为(-
,0),
∴OA=
,
∴OC=
=
=1
∴sin∠CAO=
=
,
∴∠CAO=30°.
(1)∵f(1)=
| 1 |
| 1+1 |
| 1 |
| 2 |
| 2 |
| 1+2 |
| 2 |
| 3 |
| 1 |
| 2 |
| ||
1+
|
| 1 |
| 3 |
| 3 |
| 4 |
| 1 |
| 3 |
| 1 |
| 4 |
∴f(1)=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
原式=f(1)+f(2)+f(
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2008 |
| 1 |
| 2009 |
=
| 1 |
| 2 |
=2008
| 1 |
| 2 |
(2)

∵∠AOC=90°,
∴AC是⊙B的直径,
∴AC=2
又∵点A的坐标为(-
| 3 |
∴OA=
| 3 |
∴OC=
| AC2-OA2 |
22-(
|
∴sin∠CAO=
| OC |
| AC |
| 1 |
| 2 |
∴∠CAO=30°.
点评:本题的第(1)小题,找到f(n)+f(
)=1是解题的关键,第(2)小题主要是解直角三角形.
| 1 |
| n |

练习册系列答案
相关题目