题目内容
如图,菱形ABCD中,BE⊥AD,BF⊥CD,E、F分别是垂足,AE=DE,则∠EBF是
- A.75°
- B.60°
- C.50°
- D.45°
B
试题分析:连接BD,首先推出△ABD是等边三角形,然后可知∠A=60°,∠EBF+∠D=180°,∠D+∠A=180°,故可得∠EBF=∠A=60°.
如图,连接BD,

∵BE⊥AD,AE=DE,
∴BD=AB=AD,
∴△ABD是等边三角形,
∴∠A=60°,
又∵BE⊥AD,BF⊥CD,
∴∠BED+∠BFD=180°,
∴∠D+∠EBF=180°,
又∵∠D+∠A=180°,
∴∠EBF=∠A=60°.
故选B.
考点:本题考查的是菱形的性质,等边三角形的判定和性质
点评:解答本题的关键是得到△ABD是等边三角形,熟练掌握同角的补角相等。
试题分析:连接BD,首先推出△ABD是等边三角形,然后可知∠A=60°,∠EBF+∠D=180°,∠D+∠A=180°,故可得∠EBF=∠A=60°.
如图,连接BD,

∵BE⊥AD,AE=DE,
∴BD=AB=AD,
∴△ABD是等边三角形,
∴∠A=60°,
又∵BE⊥AD,BF⊥CD,
∴∠BED+∠BFD=180°,
∴∠D+∠EBF=180°,
又∵∠D+∠A=180°,
∴∠EBF=∠A=60°.
故选B.
考点:本题考查的是菱形的性质,等边三角形的判定和性质
点评:解答本题的关键是得到△ABD是等边三角形,熟练掌握同角的补角相等。

练习册系列答案
相关题目
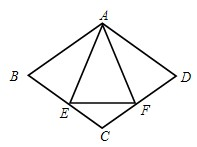 26、已知:如图,菱形ABCD中,E,F分别是CB,CD上的点,且BE=DF.
26、已知:如图,菱形ABCD中,E,F分别是CB,CD上的点,且BE=DF. 如图,菱形ABCD中,∠A=60°,AB=2,动点P从点B出发,以每秒1个单位长度的速度沿B→C→D向终点D运动.同时动点Q从点A出发,以相同的速度沿A→D→B向终点B运动,运动的时间为x秒,当点P到达点D时,点P、Q同时停止运动,设△APQ的面积为y,则反映y与x的函数关系的图象是( )
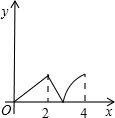
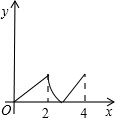
如图,菱形ABCD中,∠A=60°,AB=2,动点P从点B出发,以每秒1个单位长度的速度沿B→C→D向终点D运动.同时动点Q从点A出发,以相同的速度沿A→D→B向终点B运动,运动的时间为x秒,当点P到达点D时,点P、Q同时停止运动,设△APQ的面积为y,则反映y与x的函数关系的图象是( )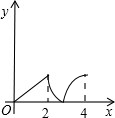
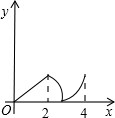
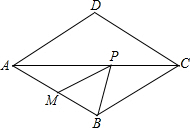 如图,菱形ABCD中,∠BAD=60°,M是AB的中点,P是对角线AC上的一个动点,若AB长为2
如图,菱形ABCD中,∠BAD=60°,M是AB的中点,P是对角线AC上的一个动点,若AB长为2 如图:菱形ABCD中,E是AB的中点,且CE⊥AB,AB=6cm.
如图:菱形ABCD中,E是AB的中点,且CE⊥AB,AB=6cm. 如图,菱形ABCD中,∠ADC=120°,AB=10,
如图,菱形ABCD中,∠ADC=120°,AB=10,