题目内容
如图,⊙A、⊙B的半径分别为4、2,且AB=12.若作⊙C使得圆心在一直线AB上,且⊙C与⊙A外切,⊙C与⊙B相交于两点,则⊙C的半径可以是
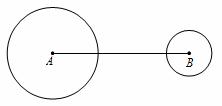
A.3 B.4 C.5 D.6
B

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
题目内容
如图,⊙A、⊙B的半径分别为4、2,且AB=12.若作⊙C使得圆心在一直线AB上,且⊙C与⊙A外切,⊙C与⊙B相交于两点,则⊙C的半径可以是

A.3 B.4 C.5 D.6
B

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案