题目内容
 点D是△ABC内一点,AD平分∠ABC,延长AD交△ABC的外接圆于点E,BE=ED.
点D是△ABC内一点,AD平分∠ABC,延长AD交△ABC的外接圆于点E,BE=ED.
(1)点D是否是△ABC的内心?说明理由;
(2)点E是否是△BDC的外心?说明理由.
 解:(1)点D是△ABC的内心.
解:(1)点D是△ABC的内心.理由是:连接CE,
∵AD平分∠ABC,
∴∠BAD=∠CAD,
∴弧BE=弧CE,
∴BE=EC,∠EBC=∠CAE=∠BAE,
∵BD=BE,
∴∠EDB=∠DBE,
即∠BAE+∠ABD=∠CBD+∠EBC,
∴∠ABD=∠CBD,
即D是∠ABC和∠BAC的角平分线的交点,
∴点D是△ABC的内心.
(2)点E是△BDC的外心.
理由是:由(1)知:BE=CE=ED,
∴点E是△BDC的外心.
分析:(1)根据角平分线性质求出BE=CE,根据三角形外角性质和等腰三角形性质推出∠CBD=∠ABD,即可得到答案;
(2)根据BE=CE=DE即可推出答案.
点评:本题主要考查对等腰三角形的性质和判定,三角形的内切圆与内心,三角形的外接圆与外心,圆心角、弧、弦之间的关系等知识点的理解和掌握,综合运用性质进行推理是解此题的关键.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
 16、如图点P是∠ABC内一点画图:
16、如图点P是∠ABC内一点画图: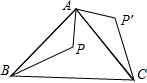 如图,△ABC是等腰直角三角形,BC是斜边,点P是△ABC内一点,△ABP绕点A逆时针旋转后与△ACP′重合,如果AP=
如图,△ABC是等腰直角三角形,BC是斜边,点P是△ABC内一点,△ABP绕点A逆时针旋转后与△ACP′重合,如果AP= 22、如图,点D是△ABC内一点,点E是△ABC外的一点,且∠1=∠2,∠3=∠4,图中有与∠ACB相等的角吗?如果有,请找出来,并说明理由.
22、如图,点D是△ABC内一点,点E是△ABC外的一点,且∠1=∠2,∠3=∠4,图中有与∠ACB相等的角吗?如果有,请找出来,并说明理由. 如图,点O是△ABC内一点,且点O到三边距离相等,∠BOC=132°,则∠A=
如图,点O是△ABC内一点,且点O到三边距离相等,∠BOC=132°,则∠A=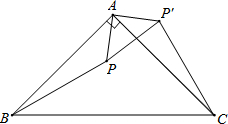 如图,在Rt△ABC中,∠CAB=90°,点P是△ABC内一点,将△ABP绕点A逆时针旋转后能与△ACP′重合,如果AP=5,求PP′的长.
如图,在Rt△ABC中,∠CAB=90°,点P是△ABC内一点,将△ABP绕点A逆时针旋转后能与△ACP′重合,如果AP=5,求PP′的长.