题目内容
9.某商店销售10台A型和20台B型电脑的利润为4000元,销售20台A型和10台B型电脑的利润为3500元.(1)求每台A型电脑和B型电脑的销售利润;
(2)该商店计划一次购进两种型号的电脑共100台,全部销售后获得的利润不低于11000元,那么A型电脑最多进货多少台?
分析 (1)设每台A型电脑的售价利润为x元,每台B型电脑的售价利润为y元,接下来依据销售10台A型和20台B型电脑的利润为4000元,销售20台A型和10台B型电脑的利润为3500元列方程组求解即可;
(2)设A型电脑进a台,则B型电脑进(100-a)台,接下来依据销售的总利润不低于11000元列不等式求解即可.
解答 解:(1)设每台A型电脑的售价利润为x元,每台B型电脑的售价利润为y元.
根据题意得:$\left\{\begin{array}{l}{10x+20y=4000}\\{20x+10y=3500}\end{array}\right.$,
解得:x=100,y=150.
答:每台A型电脑100元,每台B型电脑150元.
(2)设A型电脑进a台,则B型电脑进(100-a)台.
根据题意得:100a+150(100-a)≥11000.
解得:a≤80.
所以a的最小值为80.
答:A型电脑最多进货80台.
点评 本题主要考查的是二元一次方程组的应用和一元一次不等式的应用,根据题意列出方程组和不等式组是解题的关键.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
4.下列对方程2x-3y=7变形正确的是( )
| A. | y=$\frac{7-2x}{3}$ | B. | y=$\frac{2x-7}{3}$ | C. | x=$\frac{3y-7}{2}$ | D. | x=$\frac{7-3y}{2}$ |
1.下列说法正确的是( )
| A. | 调查重庆市空气质量情况应该采用普查的方式 | |
| B. | A组数据方差$S_A^2=0.03$,B组数据方差$S_B^2=0.2$,则B组数据比A组数据稳定 | |
| C. | 重庆八中明年开运动会一定不会下雨 | |
| D. | 2,3,6,9,5这组数据的中位数是5 |
18.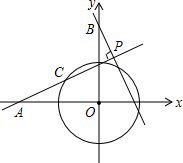 如图,在平面直角坐标系xOy中,A(-2,0),B(0,2),⊙O的半径为1,点C为⊙O上一动点,过点B作BP⊥直线AC,垂足为点P,则P点纵坐标的最大值为( )
如图,在平面直角坐标系xOy中,A(-2,0),B(0,2),⊙O的半径为1,点C为⊙O上一动点,过点B作BP⊥直线AC,垂足为点P,则P点纵坐标的最大值为( )
 如图,在平面直角坐标系xOy中,A(-2,0),B(0,2),⊙O的半径为1,点C为⊙O上一动点,过点B作BP⊥直线AC,垂足为点P,则P点纵坐标的最大值为( )
如图,在平面直角坐标系xOy中,A(-2,0),B(0,2),⊙O的半径为1,点C为⊙O上一动点,过点B作BP⊥直线AC,垂足为点P,则P点纵坐标的最大值为( )| A. | $2\sqrt{2}$ | B. | $\frac{{\sqrt{3}+1}}{2}$ | C. | 2 | D. | $\frac{3}{2}$ |
19.多项式x2-4x-12可以因式分解成( )
| A. | x(x-4)-12 | B. | (x-2)(x+6) | C. | (x+2)(x-6) | D. | (x+3)(x-4) |
 如图,△ABC沿边BC向右平移2个单位得到△DEF,已知BC=5,则EC=3.
如图,△ABC沿边BC向右平移2个单位得到△DEF,已知BC=5,则EC=3.