题目内容
4. 如图,△ABC的面积是12,点D、E、F、G分别是BC、AD、BE、CE的中点,则△AFG的面积是( )
如图,△ABC的面积是12,点D、E、F、G分别是BC、AD、BE、CE的中点,则△AFG的面积是( )| A. | 4.5 | B. | 5 | C. | 5.5 | D. | 6 |
分析 根据中线的性质,可得△AEF的面积=$\frac{1}{2}$×△ABE的面积=$\frac{1}{4}$×△ABD的面积=$\frac{1}{8}$×△ABC的面积=$\frac{3}{2}$,△AEG的面积=$\frac{3}{2}$,根据三角形中位线的性质可得△EFG的面积=$\frac{1}{4}$×△BCE的面积=$\frac{3}{2}$,进而得到△AFG的面积.
解答 解:∵点D,E,F,G分别是BC,AD,BE,CE的中点,
∴AD是△ABC的中线,BE是△ABD的中线,CF是△ACD的中线,AF是△ABE的中线,AG是△ACE的中线,
∴△AEF的面积=$\frac{1}{2}$×△ABE的面积=$\frac{1}{4}$×△ABD的面积=$\frac{1}{8}$×△ABC的面积=$\frac{3}{2}$,
同理可得△AEG的面积=$\frac{3}{2}$,
△BCE的面积=$\frac{1}{2}$×△ABC的面积=6,
又∵FG是△BCE的中位线,
∴△EFG的面积=$\frac{1}{4}$×△BCE的面积=$\frac{3}{2}$,
∴△AFG的面积是$\frac{3}{2}$×3=$\frac{9}{2}$,
故选:A.
点评 本题主要考查了三角形的面积,解决问题的关键是掌握:三角形的中线将三角形分成面积相等的两部分.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.我市某连续7天的最高气温为:28°,27°,30°,33°,30°,30°,32°,这组数据的平均数和众数分别是( )
| A. | 28°,30° | B. | 30°,28° | C. | 31°,30° | D. | 30°,30° |
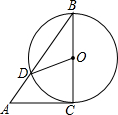 如图,AC是⊙O的切线,切点为C,BC是⊙O的直径,AB交⊙O于点D,连接OD,若∠A=50°,则∠COD的度数为80°.
如图,AC是⊙O的切线,切点为C,BC是⊙O的直径,AB交⊙O于点D,连接OD,若∠A=50°,则∠COD的度数为80°. 如图,在矩形ABCD中,AB=3,AD=5,点E在DC上,将矩形ABCD沿AE折叠,点D恰好落在BC边上的点F处,那么cos∠EFC的值是$\frac{3}{5}$.
如图,在矩形ABCD中,AB=3,AD=5,点E在DC上,将矩形ABCD沿AE折叠,点D恰好落在BC边上的点F处,那么cos∠EFC的值是$\frac{3}{5}$. .
.