题目内容
如图,已知抛物线的对称轴为直线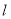 :
: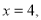 且与
且与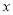 轴交于点
轴交于点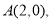 与
与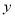 轴交于点
轴交于点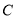
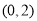 .
.
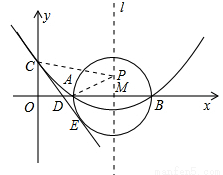
(1)求抛物线的解析式;
(2)试探究在此抛物线的对称轴 上是否存在一点
上是否存在一点 ,使
,使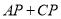 的值最小?若存在,求
的值最小?若存在,求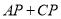 的最小值,若不存在,请说明理由;
的最小值,若不存在,请说明理由;
(3)以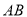 为直径作⊙
为直径作⊙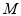 ,过点
,过点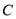 作直线
作直线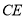 与⊙
与⊙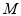 相切于点
相切于点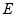 ,
,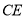 交
交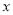 轴于点
轴于点 ,求直线
,求直线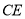 的解析式.
的解析式.
【解析】
(1)如图,由题意,设抛物线的解析式为:
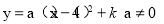
∵抛物线经过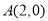 、
、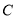
 .
.
∴
解得:a=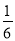 ,
,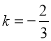 .
.
∴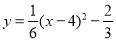 ,
,
即: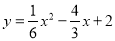 .
.
(2)存在.
令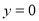 , 得
, 得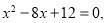
即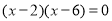 ,
,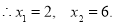
 抛物线与
抛物线与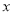 轴的另-交点
轴的另-交点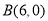 .
.
如本题图2,连接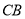 交
交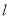 于点
于点 ,则点
,则点 即是使
即是使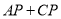 的值最小的点.
的值最小的点.

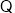 因为
因为 关于
关于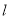 对称,则
对称,则 ,
, ,即
,即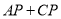 的最小值为
的最小值为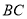 .
.
∵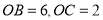 ,
,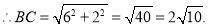
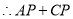 的最小值为
的最小值为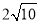 ;
;
(3)如图3,连接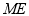 ,∵
,∵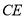 是⊙
是⊙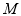 的切线,
的切线,

∴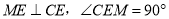 ,
,
由题意,得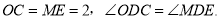
∵在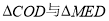 中,
中,
 ,
,
∴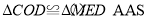 ,
,
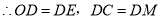 ,
,
设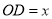 ,则
,则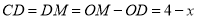 ,
,
则在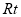 △
△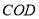 中,又
中,又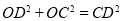 ,
,
∴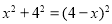 ,解得
,解得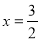 ,
,
∴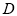 (
(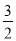 ,0)
,0)
设直线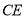 的解析式为
的解析式为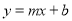 ,∵直线
,∵直线 过
过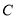 (0,2)、
(0,2)、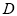 (
(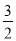 ,0)两点,
,0)两点,

 ,解方程组得:
,解方程组得: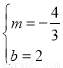 .
.
∴直线 的解析式为
的解析式为
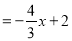 .
.
【解析】
试题分析:(1)根据题意设抛物线的解析式为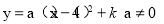 ,将
,将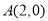 、
、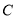
 代入解析式,即可求出a,k的值,得出抛物线的解析式,令
代入解析式,即可求出a,k的值,得出抛物线的解析式,令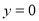 ,即可求出抛物线与
,即可求出抛物线与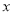 轴另-交点
轴另-交点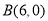 ;(2)连接
;(2)连接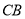 交
交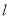 于点
于点 ,则点
,则点 即是使
即是使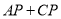 的值最小的点. 则
的值最小的点. 则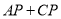 的最小值为
的最小值为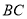 ,在Rt△OBC中,根据勾股定理即可求出BC的值;(3)连接
,在Rt△OBC中,根据勾股定理即可求出BC的值;(3)连接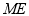 ,根据已知条件可得
,根据已知条件可得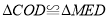 ,根据全等三角形的对应边相等可得
,根据全等三角形的对应边相等可得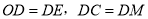 ,在
,在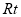 △
△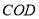 中,根据勾股定理求出OD,即可得出D点坐标,设直线
中,根据勾股定理求出OD,即可得出D点坐标,设直线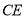 的解析式为
的解析式为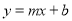 ,代入C,D两点坐标,即可解得直线
,代入C,D两点坐标,即可解得直线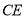 的解析式.
的解析式.
考点:二次函数的综合题.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目

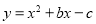 与
与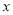 轴交
轴交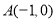 、
、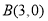 两点,直线
两点,直线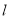 与抛物线交于A、C两点,其中C点的横坐标为2.
与抛物线交于A、C两点,其中C点的横坐标为2.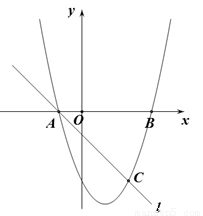
 轴的平行线交抛物线于F点,求线段PF长度的最大值.
轴的平行线交抛物线于F点,求线段PF长度的最大值. cm,那么围成的圆锥的高度是
cm,那么围成的圆锥的高度是
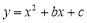 的图象过点(4,3)、(3,0).
的图象过点(4,3)、(3,0).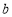 、
、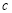 的值;
的值;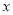 取何值时,
取何值时,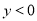 ?
?
 的解为 .
的解为 .