题目内容
14. 如图,已知⊙O的直径CD=5cm,AB是⊙O的弦,AB⊥CD,垂足为M,若OM:DM=3:8,则AB的长度为4.
如图,已知⊙O的直径CD=5cm,AB是⊙O的弦,AB⊥CD,垂足为M,若OM:DM=3:8,则AB的长度为4.
分析 如图,连接OA;首先求出OM的长;运用勾股定理求出AM的长度,借助垂径定理证明AM=BM,即可解决问题.
解答  解:如图,连接OA;
解:如图,连接OA;
∵OM:DM=3:8,
∴OM:OD=3:5;而OD=2.5,
∴OM=1.5;由勾股定理得:
AM2=OA2-OM2,而OA=2.5,
∴AM=2;而AB⊥CD,
∴AM=BM,AB=2AM=4.
故答案为4.
点评 该题主要考查了勾股定理、垂径定理等知识点的应用问题;牢固掌握勾股定理等几何知识点是解题的关键.

练习册系列答案
相关题目
5.2014年五一“黄金周”全市接待游客总数为996000人次.将数996000用科学记数法表示应为( )
| A. | 0.996×106 | B. | 96.6×105 | C. | 9.96×105 | D. | 9.96×104 |
2.据报道,肇庆团市委“情系农村”深化农村青年创业小额贷款工作,共发放贷款13 000 000多元,数字13 000 000用科学记数法表示为( )
| A. | 1.3×106 | B. | 1.3×107 | C. | 1.3×108 | D. | 1.3×109 |
9.若$\sqrt{a}$=a,则a的值为( )
| A. | 1 | B. | -1 | C. | 0或1 | D. | ±1 |
 如图,若把太阳看成一个圆,则太阳与地平线l的位置关系是相交(填“相交”、“相切”、“相离”).
如图,若把太阳看成一个圆,则太阳与地平线l的位置关系是相交(填“相交”、“相切”、“相离”).
 如图,弦AB与⊙O相交于A、B两点,已知⊙O的直径为10,若圆心O到AB的距离为3,那么弦AB长为8.
如图,弦AB与⊙O相交于A、B两点,已知⊙O的直径为10,若圆心O到AB的距离为3,那么弦AB长为8.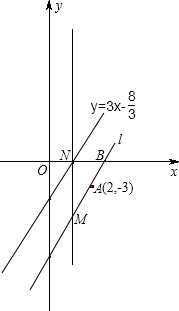 如图,在平面直角坐标系中,直线l经过点A(2,-3),与x轴交于点B,且与直线$y=3x-\frac{8}{3}$平行.
如图,在平面直角坐标系中,直线l经过点A(2,-3),与x轴交于点B,且与直线$y=3x-\frac{8}{3}$平行.