题目内容
如图,已知直线 交⊙O于A、B两点,AE是⊙O的直径,点C为⊙O上一点,且AC平分∠PAE,过C作
交⊙O于A、B两点,AE是⊙O的直径,点C为⊙O上一点,且AC平分∠PAE,过C作 ,垂足为D.
,垂足为D.【小题1】(1) 求证:CD为⊙O的切线;
【小题2】(2) 若CD=2AD,⊙O的直径为10,求线段AC的长.

src="https://thumb.zyjl.cn/pic1/imagenew2/czsx/15/54615.png" >【答案】

【小题1】(1)证明:连接OC.
∵ 点C在⊙O上,OA=OC,
∴
∵ ,
,
∴ ,有
,有 .
.
∵AC平分∠PAE,
∴
∴ ……………………………………1分
……………………………………1分
∴
∵ 点C在⊙O上,OC为⊙O的半径,
∴ CD为⊙O的切线.
【小题2】(2)解:连结CE.
∵ AE是⊙O的直径,
∴ .
.
∴ .
.
又∵ ,
,
∴ ∽
∽ .………………3分
.………………3分
∴ .
.
又∵ CD=2AD ,
∴ CE=2AC. ……………………………………4分
设AC=x .
在 中,由勾股定理知
中,由勾股定理知
∵ AE=10,
∴
解得 .
.
∴ . 解析:
. 解析:
略

【小题1】(1)证明:连接OC.
∵ 点C在⊙O上,OA=OC,
∴

∵
 ,
,∴
 ,有
,有 .
.∵AC平分∠PAE,
∴

∴
 ……………………………………1分
……………………………………1分∴

∵ 点C在⊙O上,OC为⊙O的半径,
∴ CD为⊙O的切线.
【小题2】(2)解:连结CE.
∵ AE是⊙O的直径,
∴
 .
.∴
 .
.又∵
 ,
,∴
 ∽
∽ .………………3分
.………………3分∴
 .
.又∵ CD=2AD ,
∴ CE=2AC. ……………………………………4分
设AC=x .
在
 中,由勾股定理知
中,由勾股定理知
∵ AE=10,
∴

解得
 .
. ∴
 . 解析:
. 解析:略

练习册系列答案
相关题目
 如图,已知直线
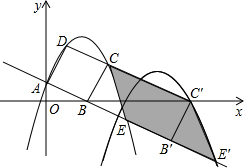
如图,已知直线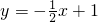 交坐标轴于A、B点,以线段AB为边向上作正方形ABCD,过点A、D、C的抛物线与直线的另一个交点为E.
交坐标轴于A、B点,以线段AB为边向上作正方形ABCD,过点A、D、C的抛物线与直线的另一个交点为E.
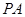 交⊙O于A、B两点,AE是⊙O的直径,点C为⊙O 上一点,过C作
交⊙O于A、B两点,AE是⊙O的直径,点C为⊙O 上一点,过C作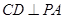 ,垂足为D。问:当AC满足什么条件时,CD为⊙O的切线,请说明理由。
,垂足为D。问:当AC满足什么条件时,CD为⊙O的切线,请说明理由。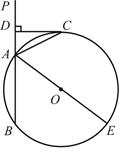

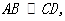 直线
直线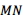 交
交 于
于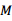 ,交
,交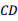 于
于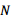 ,
,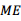 平分
平分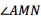 ,
,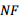 平分
平分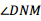
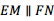
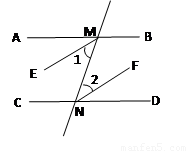
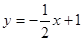 交坐标轴于A,B两点,以线段AB为边向上作正方形ABCD,过点A,D,C的抛物线与直线另一个交点为E.
交坐标轴于A,B两点,以线段AB为边向上作正方形ABCD,过点A,D,C的抛物线与直线另一个交点为E.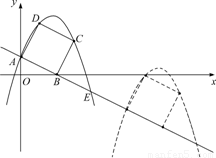
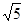 个单位长度的速度沿射线AB下滑,直至顶点D落在x轴上时停止.设正方形落在x轴下方部分的面积为S,求S关于滑行时间t的函数关系式,并写出相应自变量t的取值范围
个单位长度的速度沿射线AB下滑,直至顶点D落在x轴上时停止.设正方形落在x轴下方部分的面积为S,求S关于滑行时间t的函数关系式,并写出相应自变量t的取值范围