题目内容
已知函数y=a(x-h)2+k是由y=
x2向上平移2个单位,再向右平移1个单位,得到的抛物线.
(1)求a、h、k;
(2)当x取何值时,y随x增大而增大;
(3)试求y的取值范围.
| 1 |
| 2 |
(1)求a、h、k;
(2)当x取何值时,y随x增大而增大;
(3)试求y的取值范围.
考点:二次函数图象与几何变换
专题:
分析:(1)易得原抛物线的顶点及平移后新抛物线的顶点,根据平移不改变二次项系数利用顶点式可得抛物线解析式;
(2)根据抛物线的对称轴、抛物线的增减性进行解答;
(3)根据抛物线的开口方向、顶点坐标进行分析解答.
(2)根据抛物线的对称轴、抛物线的增减性进行解答;
(3)根据抛物线的开口方向、顶点坐标进行分析解答.
解答:解:(1)∵函数y=
x2的顶点为(0,0),
∴向上平移2个单位,再向右平移1个单位的顶点为(1,2),
∴将函数y=
x2的图象向上平移2个单位,再向右平移1个单位,得到抛物线的解析式为y=
(x-1)2+2,
∴函数y=a(x-h)2+k中的a=
,h=1,k=2;
(2)由(1)知,平移后的抛物线解析式为y=
(x-1)2+2,则该抛物线的开口方向向上,对称轴是x=1.
故当x>1时,y随x增大而增大;
(3)由(1)知,平移后的抛物线解析式为y=
(x-1)2+2,则抛物线的开口方向向上,顶点坐标是(1,2),
则y≥2.
| 1 |
| 2 |
∴向上平移2个单位,再向右平移1个单位的顶点为(1,2),
∴将函数y=
| 1 |
| 2 |
| 1 |
| 2 |
∴函数y=a(x-h)2+k中的a=
| 1 |
| 2 |
(2)由(1)知,平移后的抛物线解析式为y=
| 1 |
| 2 |
故当x>1时,y随x增大而增大;
(3)由(1)知,平移后的抛物线解析式为y=
| 1 |
| 2 |
则y≥2.
点评:此题主要考查二次函数的平移情况;用到的知识点为:二次函数的平移不改变二次项的系数;关键是根据上下平移改变顶点的纵坐标,左右平移改变顶点的横坐标得到新抛物线的顶点.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知关于x的方程5x+3k=21与5x+3=0的解相同,则k的值是( )
| A、-10 | B、7 | C、-9 | D、8 |
 2000年~2005年某市城市居民人均可支配收入情况(如图).
2000年~2005年某市城市居民人均可支配收入情况(如图).
 将-8,-6,-4,-2,0,2,4,6,8这9个数分别填如图的9个空格中,使得横,竖,斜对角的3个数相加的和为0,怎么填?
将-8,-6,-4,-2,0,2,4,6,8这9个数分别填如图的9个空格中,使得横,竖,斜对角的3个数相加的和为0,怎么填?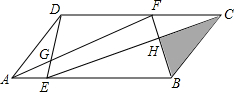 图中ABCD是平行四边形,面积是1,F为DC边上一点,E为AB上一点,连接AF,BF,DE,CE,AF交DE于G,EC交FB于H.已知,
图中ABCD是平行四边形,面积是1,F为DC边上一点,E为AB上一点,连接AF,BF,DE,CE,AF交DE于G,EC交FB于H.已知,