题目内容
15.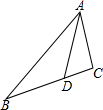 如图,在△ABC中,点D在边BC上,若∠BAD=∠CAD,AB=6,AC=3,S△ABD=3,则S△ACD=$\frac{3}{2}$.
如图,在△ABC中,点D在边BC上,若∠BAD=∠CAD,AB=6,AC=3,S△ABD=3,则S△ACD=$\frac{3}{2}$.
分析 过D作DP⊥AC交AC的延长线于P,DQ⊥AB于Q,根据角平分线的性质得到DP=DQ,根据S△ABD=$\frac{1}{2}$AB•DQ=$\frac{1}{2}×6$•DQ=3,求得DQ=1,得到DP=1,即可得到结论.
解答 解:过D作DP⊥AC交AC的延长线于P,DQ⊥AB于Q,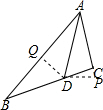
∵∠BAD=∠CAD,
∴DP=DQ,
∵S△ABD=$\frac{1}{2}$AB•DQ=$\frac{1}{2}×6$•DQ=3,
∴DQ=1,
∴DP=1,
∴S△ACD=$\frac{1}{2}$•AC•DP=$\frac{3}{2}$,
故答案为:$\frac{3}{2}$.
点评 本题考查了角平分线的性质,三角形的面积的计算,正确的作出辅助线是解题的关键.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案
相关题目
20.已知:∠A=25°12′,∠B=25.12°,∠C=25.2°,下列结论正确的是( )
| A. | ∠A=∠B | B. | ∠B=∠C | C. | ∠A=∠C | D. | 三个角互不相等 |
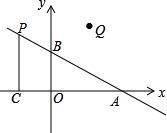 如图,在平面直角坐标系中,O是坐标原点,点A的坐标为(4,0),点B的坐标为(0,b)(b>0),点P是直线AB上位于第二象限内的一个动点,过点P作PC⊥x轴于点C,记点P关于y轴的对称点为Q,设点P的横坐标为a.
如图,在平面直角坐标系中,O是坐标原点,点A的坐标为(4,0),点B的坐标为(0,b)(b>0),点P是直线AB上位于第二象限内的一个动点,过点P作PC⊥x轴于点C,记点P关于y轴的对称点为Q,设点P的横坐标为a. 已知有理数a,b在数轴上的位置如图所示.
已知有理数a,b在数轴上的位置如图所示.