题目内容
10.(1)计算:$\sqrt{18}$-(2$\sqrt{75}$-$\sqrt{27}$)(2)先化简,再求值:($\frac{x}{x+2}$-$\frac{{x}^{2}-4x+4}{{x}^{2}-4}$)÷$\frac{x}{x-2}$,其中x=$\sqrt{2}$.
分析 (1)原式去括号化简后,合并同类二次根式即可得到结果;
(2)原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分得到最简结果,把x的值代入计算即可求出值.
解答 解:原式=3$\sqrt{2}$-10$\sqrt{3}$+3$\sqrt{3}$=3$\sqrt{2}$-7$\sqrt{3}$;
(2)原式=$\frac{{x}^{2}-2x-{x}^{2}+4x-4}{(x+2)(x-2)}$•$\frac{x-2}{x}$=$\frac{2(x-2)}{x+2}$•$\frac{1}{x}$=$\frac{2x-4}{{x}^{2}+2x}$,
当x=$\sqrt{2}$时,原式=$\frac{2\sqrt{2}-4}{2+2\sqrt{2}}$=$\frac{12-16\sqrt{2}}{4}$=3-4$\sqrt{2}$.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
18.抛物线y=ax2+bx+c(a≠0)上部分点的横、纵坐标的对应值如下表:
则该抛物线的顶点坐标为(2,-4).
| x | … | -1 | 0 | 1 | 2 | 3 | 4 | … |
| y | … | 14 | 4 | -2 | -4 | -2 | 4 | … |
19.下列事件是确定事件的是( )
| A. | 任意打开一本200页的数学书,恰好是第50页 | |
| B. | 打开电视机,任选一个频道,正在播放足球赛 | |
| C. | 在空旷的操场上向上抛出的篮球一定会下落 | |
| D. | 阴天一定会下雨 |

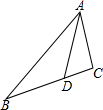 如图,在△ABC中,点D在边BC上,若∠BAD=∠CAD,AB=6,AC=3,S△ABD=3,则S△ACD=$\frac{3}{2}$.
如图,在△ABC中,点D在边BC上,若∠BAD=∠CAD,AB=6,AC=3,S△ABD=3,则S△ACD=$\frac{3}{2}$.