题目内容
(x2-mx+3)(3x-2)的积中不含x的二次项,则m的值是
- A.0
- B.

- C.-

- D.-

C
分析:根据多项式乘多项式的法则先把原式展开得出3x3+(-2-3m)x2+(2m+9)x-6,根据已知积中不含x的二次项得出方程-2-3m=0,求出方程的解即可.
解答:(x2-mx+3)(3x-2),
=3x3-2x2-3mx2+2mx+9x-6,
=3x3+(-2-3m)x2+(2m+9)x-6,
∵(x2-mx+3)(3x-2)的积中不含x的二次项,
∴-2-3m=0,
解得:m=- ,
,
故选C.
点评:本题考查了多项式乘多项式和解一元一次方程的应用,关键是根据题意得出方程-2-3m=0,题型较好,主要培养学生的理解能力和计算能力.
分析:根据多项式乘多项式的法则先把原式展开得出3x3+(-2-3m)x2+(2m+9)x-6,根据已知积中不含x的二次项得出方程-2-3m=0,求出方程的解即可.
解答:(x2-mx+3)(3x-2),
=3x3-2x2-3mx2+2mx+9x-6,
=3x3+(-2-3m)x2+(2m+9)x-6,
∵(x2-mx+3)(3x-2)的积中不含x的二次项,
∴-2-3m=0,
解得:m=-
 ,
,故选C.
点评:本题考查了多项式乘多项式和解一元一次方程的应用,关键是根据题意得出方程-2-3m=0,题型较好,主要培养学生的理解能力和计算能力.

练习册系列答案
相关题目
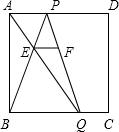 EF平行BC交PQ于F,AP、BQ分别为方程x2-mx+n=0的两根.
EF平行BC交PQ于F,AP、BQ分别为方程x2-mx+n=0的两根.